Bài 8 trang 128 SGK Hình học 10 nâng caoViết phương trình đường thẳng Δ đi qua M, N và tìm các giao điểm P, Q của Δ với hai đường tiệm cận của hypebol (H) Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Cho hypebol (H) có phương trình \({{{x^2}} \over {16}} - {{{y^2}} \over 4} = 1\) LG a Viết phương trình các đường tiệm cận của hypebol (H). Lời giải chi tiết: Ta có: a2 =16; b2 = 4 => a= 4 và b = 2. Phương trình các đường tiệm cận của hypebol (H) là \(y = \pm {b \over a}x = \pm {1 \over 2}x\) LG b Tính diện tích hình chữ nhật cơ sở của hypebol (H). Lời giải chi tiết: Diện tích hình chữ nhật cơ sở của hypebol (H) là \(S = 4ab = 4.4.2 = 32\) LG c Chứng minh rằng các điểm \(M\left( {5\,;\,{3 \over 2}} \right)\,,\,N(8\,;\,2\sqrt 3 )\) đều thuộc (H). Lời giải chi tiết: Ta có \({{{5^2}} \over {16}} - {{{{\left( {{3 \over 2}} \right)}^2}} \over 4} = 1\) và \({{{8^2}} \over {16}} - {{{{\left( {2\sqrt 3 } \right)}^2}} \over 4} = 1\) nên M và N đều thuộc (H). LG d Viết phương trình đường thẳng Δ đi qua M, N và tìm các giao điểm P, Q của Δ với hai đường tiệm cận của hypebol (H). Lời giải chi tiết: Phương trình đường thẳng của MN \(\Delta \,:\,\,{{x - 5} \over {8 - 5}} = {{y - {3 \over 2}} \over {2\sqrt 3 - {3 \over 2}}}\) \(\Leftrightarrow {{x - 5} \over 3} = {{2y - 3} \over {4\sqrt 3 - 3}}\) Giao điểm P của Δ với tiệm cận \(y = {1 \over 2}x\) là nghiệm của hệ \(\left\{ \matrix{ \(\Rightarrow \,\,P\,\left( {8 + 2\sqrt 3 \,;\,\,4 + \sqrt 3 } \right)\) . Giao điểm Q của Δ với tiệm cận \(y = - {1 \over 2}x\) là nghiệm của hệ \(\left\{ \matrix{ \(\Rightarrow Q\left( {5 - 2\sqrt 3 \,;\, - {5 \over 2} + \sqrt 3 } \right)\) Cách khác:
LG e Chứng minh rằng các trung điểm của hai đoạn thẳng PQ và MN trùng nhau. Lời giải chi tiết:
Vậy các trung điểm của hai đoạn thẳng PQ và MN trùng nhau. Loigiaihay.com
|















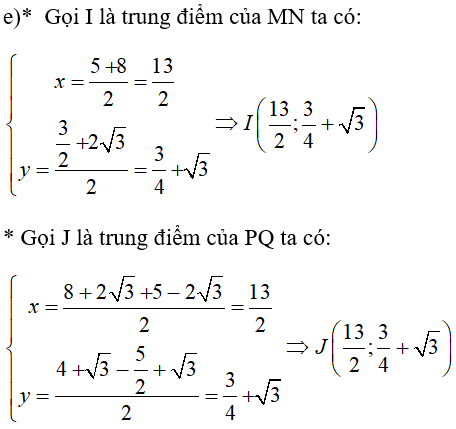






Danh sách bình luận