Bài 7 trang 114 SGK Hình học 11

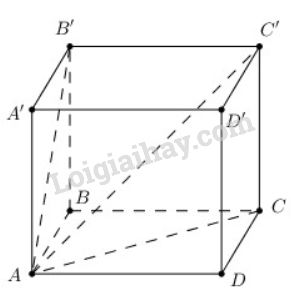
Đề bài

Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a, BC = b, CC' = c\).

a) Chứng minh rằng mặt phẳng \((ADC'B')\) vuông góc với mặt phẳng \((ABB'A')\).

b) Tính độ dài đường chéo \(AC'\) theo \(a, b, c\).

Lời giải chi tiết

a) Ta có:

\(\left\{ \begin{array}{l}
DA \bot AA'\\
DA \bot AB
\end{array} \right. \Rightarrow DA \bot \left( {ABB'A'} \right)\)

Mà \(DA ⊂ (ADC'B')\)

\(\Rightarrow (ADC'B') \bot(ABB'A')\).

b)

\(\left\{ \begin{array}{l}
C'C \bot CD\\
C'C \bot CB
\end{array} \right. \Rightarrow C'C \bot \left( {ABCD} \right)\)

Mà \(CA \subset \left( {ABCD} \right) \Rightarrow C'C \bot CA\) hay tam giác \(ACC'\) vuông tại \(C\).

Xét tam giác vuông \(ACC'\)

\(AC' = \sqrt {A{C^2} + CC{'^2}}  \) \(= \sqrt {A{D^2} + D{C^2} + CC{'^2}}\)

\(=\sqrt{a^{2}+b^{2}+c^{2}}.\)

Ghi nhớ: Hai mặt phẳng vuông góc với nhau khi mặt này chứa một đường thẳng vuông góc với mặt kia.

Loigiaihay.com