Bài 7 trang 105 SGK Hình học 11

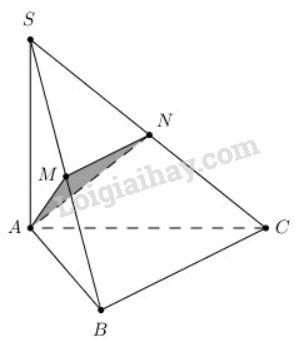
Đề bài

Cho tứ diện $SABC$ có cạnh $SA$ vuông góc với mặt phẳng $(ABC)$ và có tam giác $ABC$ vuông tại $B$. Trong mặt phẳng $(SAB)$ kẻ $AM$ vuông góc với $SB$ tại $M$. Trên cạnh $SC$ lấy điểm $N$ sao cho $\dfrac{SM}{SB}=\dfrac{SN}{SC}.$ Chứng minh rằng:

a) $BC ⊥ (SAB)$ và $AM ⊥ (SBC)$;

b) $SB ⊥ AN$.

Lời giải chi tiết

a) $SA ⊥ (ABC) \Rightarrow SA ⊥ BC$    (1),

Tam giác $ABC$ vuông tại $B$ nên $BC ⊥ AB$    (2)

Từ (1) và (2) suy ra $BC ⊥ (SAB)$.

 $BC ⊥ (SAB)$ nên $BC ⊥ AM$  (3)

$AM ⊥ SB$ (giả thiết)                    (4)

Từ (3) và (4) suy ra $AM ⊥ (SBC)$.

b) $AM ⊥ (SBC)$ nên $AM\bot SB$    (5)

$\dfrac{SM}{SB}=\dfrac{SN}{SC}$ nên theo định lí ta lét ta có: $MN// BC$

$BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB$

Ta có: 

$\left\{ \begin{array}{l} BC \bot SB\\ BC//MN \end{array} \right. \Rightarrow MN \bot SB$  (6)

Từ (5) và (6) suy ra $SB\bot (AMN)$ suy ra $SB\bot AN$

Nhận xét: Hình chóp trong các bài 4; 6; 7 thuộc loại hình chóp có một cạnh bên vuông góc với đáy (do đó nó có hai mặt bên vuông góc với đáy).

Loigiaihay.com