Bài 65 trang 112 SBT Hình học 10 Nâng cao

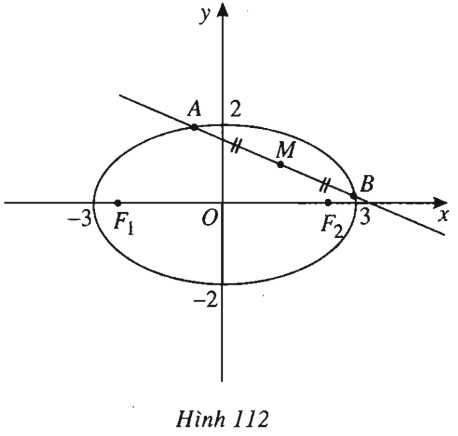
LG a

 Tìm tọa độ các tiêu điểm, các đỉnh; tính tâm sai và vẽ elip \((E)\).

Lời giải chi tiết:

\({a^2} = 9   \Rightarrow   a = 3 ,\) \(  {b^2} = 4   \Rightarrow   b = 2 ,\) \(  {c^2} = {a^2} - {b^2} = 5   \Rightarrow   c = \sqrt 5 \).

Các tiêu điểm : \({F_1}( - \sqrt 5  ; 0) ,{F_2}(\sqrt 5  ; 0) \).

Các đỉnh: \(( \pm 3 ; 0) ,  (0 ;  \pm 2)\).

Tâm sai : \(e =  \dfrac{{\sqrt 5 }}{3}\).

Elip được vẽ như hình 112.

LG b

Xác định m để đường thẳng \(d: y=x+m\) và \((E)\) có điểm chung

Lời giải chi tiết:

Hoành độ giao điểm của \(d\) và \((E)\) là nghiệm của phương trình:

\( \dfrac{{{x^2}}}{9} +  \dfrac{{{{(x + m)}^2}}}{4} = 1\)

\(    \Leftrightarrow   13{x^2} + 18mx + 9{m^2} - 36 = 0 \,\,\,\,\,\,\,  (1)\)

\(D\) và \((E)\) có điểm chung khi và chỉ khi (1) có nghiệm \( \Leftrightarrow   \Delta ' \ge 0\)

\( \Leftrightarrow   81{m^2} - 13(9{m^2} - 36) \ge 0  \)

\( \Leftrightarrow   {m^2} \le 13   \Leftrightarrow    - \sqrt {13}  \le m \le \sqrt {13} \).

Vậy với \( - \sqrt {13}  \le m \le \sqrt {13} \) thì \(d\) và \((E)\) có điểm chung.

LG c

Viết phương trình đường thẳng \(\Delta \) đi qua \(M(1 ; 1)\) và cắt \((E)\) tại hai điểm \(A, B\) sao cho \(M\) là trung điểm của đoạn thẳng \(AB\).

Lời giải chi tiết:

(h.112). Đường thẳng \(\Delta \) đi qua M, với vec tơ chỉ phương \(\overrightarrow u (a ; b)\) có dạng:

\(\left\{ \begin{array}{l}x = 1 + at\\y = 1 + bt\end{array} \right. \,\,\,\,\,({a^2} + {b^2} \ne 0)\)

\(A, B  \in \Delta     \Rightarrow    \left\{ \begin{array}{l}{x_A} = 1 + a{t_1}\\{y_A} = 1 + b{t_1}\end{array} \right.\)  và  \(\left\{ \begin{array}{l}{x_B} = 1 + a{t_2}\\{y_B} = 1 + b{t_2}\end{array} \right.\).

\(M\) là trung điểm của \(AB\) khi và chỉ khi \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}\\{y_A} + {y_B} = 2{y_M}\end{array} \right.    \Leftrightarrow    \left\{ \begin{array}{l}a({t_1} + {t_2}) = 0\\b({t_1} + {t_2}) = 0\end{array} \right.\)

\( \Leftrightarrow   {t_1} + {t_2} = 0              (1)  \)     (do \({a^2} + {b^2} \ne 0\)).

\(A, B  \in (E)\) suy ra \({t_1}, {t_2}\) là nghiệm của phương trình:

\(\begin{array}{l}4{(at + 1)^2} + 9{(bt + 1)^2} = 36   \\ \Leftrightarrow     (4 {a^2} + 9{b^2}){t^2} + (8a + 18b)t - 23 = 0.\\{t_1} + {t_2} = 0 \\   \Rightarrow    8a + 18b = 0  \\  \Leftrightarrow   4a + 9b = 0.\end{array}\)

Chọn \(a=9, b=-4,\) ta được phương trình của \(\Delta :  \left\{ \begin{array}{l}x = 1 + 9t\\y = 1 - 4t\end{array} \right.\) hay \(4x + 9y - 13 = 0\).

Loigiaihay.com