Bài 63 trang 92 SGK Toán 9 tập 2

Đề bài

Vẽ các hình lục giác đều, hình vuông, hình tam giác đều cùng nội tiếp đường tròn \((O;R)\) rồi tính cạnh của các hình đó theo \(R\).

Lời giải chi tiết

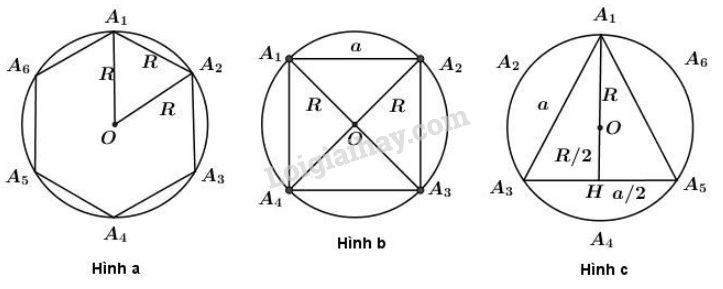
+) Hình a. 

Cách vẽ: vẽ đường tròn \((O;R)\). Trên đường tròn ta đặt liên tiếp các cung \(\overparen{{A_1}{A_2}}\),  \(\overparen{{A_2}{A_3}}\),...,\(\overparen{{A_6}{A_1}}\) mà dây căng cung có độ dài bằng \(R\). Nối \({A_1}\) với \({A_2}\), \({A_2}\) với \({A_3}\),…, \({A_6}\) với \({A_1}\) ta được hình lục giác đều \({A_1}\)\({A_2}\)\({A_3}\)\({A_4}\)\({A_5}\)\({A_6}\) nội tiếp đường tròn

Tính bán kính:

Gọi \({a_i}\)  là cạnh của đa giác đều có \(i\) cạnh.

\({a_6}= R\) (vì \(O{A_1}{A_2}\) là tam giác đều)

+) Hình b.

Cách vẽ:

+ Vẽ đường kính \(A_1A_3\) của đường tròn tâm O.

+ Vẽ đường kính \(A_2A_4 ⊥A_1A_3\)

Tứ giác \(A_1A_2A_3A_4\) có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm mỗi đường nên là hình vuông.

Nối \(A_1\) với \(A_2;A_2\) với \(A_3;A_3\) với \(A_4;A_4\) với \(A_1\) ta được hình vuông \(A_1A_2A_3A_4\) nội tiếp đường tròn (O). 

Tính bán kính:

Gọi độ dài cạnh của hình vuông là \(a.\)

Vì hai đường chéo của hình vuông vuông góc với nhau nên xét tam giác vuông \(O{A_1}{A_2}\) có

\({a^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow a = R\sqrt 2 \)

+) Hình c: 

Cách vẽ như câu a) hình a. 

Nối các điểm chia cách nhau một điểm thì ta được tam giác đều chẳng hạn tam giác \({A_1}{A_3}{A_5}\)  như trên hình c.

Tính bán kính: 

Gọi độ dài cạnh của tam giác đều  là \(a.\) 

\({A_1}H\) \(=A_1O+OH= R+\dfrac{R}{2}\) =  \(\dfrac{3R}{2}\)

\({A_3}H\) \(= \dfrac{AA'}{2}=\dfrac{a}{2}\)  

\({A_1}\)\({A_3}=a\)

Trong tam giác vuông \({A_1}H{A_3}\) ta có: \({A_1}{H^2} = {A_1}{A_3}^2 - {A_3}{H^2}\).

Từ đó \(\dfrac{9R^{2}}{4}\) = \(a^2\) - \(\dfrac{a^{2}}{4}\). 

\(\Rightarrow{a^2} = 3{R^2} \Rightarrow a = R\sqrt 3 \)

Loigiaihay.com