Bài 63 trang 102 SGK Đại số 10 nâng cao

Đề bài

Tìm a, b và c để Parabol y = ax² + bx + c có đỉnh là I(1; -4) và đi qua điểm M(2; -3). Hãy vẽ Parabol nhận được.

Lời giải chi tiết

\(I(1, -4)\) là đỉnh của Parabol nên: 

\(\left\{ \matrix{
- {b \over {2a}} = 1 \hfill \cr 
- 4 = a + b + c \hfill \cr} \right.\)

\(M(2, -3)\) thuộc parabol nên: \(-3 = 4a + 2b + c\)

 

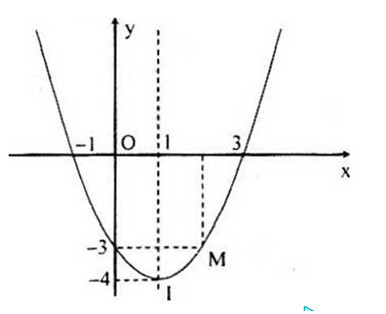
Ta có hệ:

\(\left\{ \matrix{
2a + b = 0 \hfill \cr 
a + b + c = - 4 \hfill \cr 
4a + 2b + c = - 3 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = 1 \hfill \cr 
b = - 2 \hfill \cr 
c = - 3 \hfill \cr} \right.\)

Vậy \(y = x^2 – 2x – 3\)

Đồ thị hàm số: \(y = x^2 – 2x – 3\)

Loigiaihay.com