Bài 62 trang 48 SBT Hình học 10 Nâng cao

Đề bài

Tìm quỹ tích những điểm có tổng bình phương các khoảng cách đến bốn đỉnh của một tứ giác bằng \(k^2\) không đổi.

Lời giải chi tiết

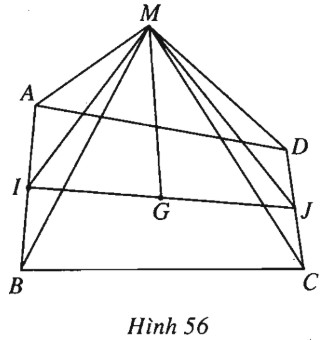
Xét tứ giác \(ABCD\). Gọi \(I, J\) lần lượ là trung điểm của \(AB, CD\) và \(G\) là trung điểm cùa \(IJ\) (h.56). Với mỗi điểm \(M,\) ta đều có:

\(\begin{array}{l}M{A^2} + M{B^2} + M{C^2} + M{D^2}\\ = 2M{I^2} + \dfrac{{A{B^2}}}{2} + 2M{J^2} + \dfrac{{C{D^2}}}{2}\\= 2\left( {2M{G^2} + \dfrac{{I{J^2}}}{2}} \right) + \dfrac{{A{B^2} + C{D^2}}}{2}\\= 4M{G^2} + \dfrac{{A{B^2} + C{D^2}}}{2} + I{J^2}.\end{array}\)

Từ đó suy ra

\(M{A^2} + M{B^2} + M{C^2} + M{D^2}\)

\(= {k^2} \Leftrightarrow   4M{G^2}\)

\(= {k^2} - \left( {\dfrac{{A{B^2} + C{D^2}}}{2} + I{J^2}} \right)\) không đổi.

Từ đó ta có:

Nếu \({k^2} - \left( {\dfrac{{A{B^2} + C{D^2}}}{2} + I{J^2}} \right) > 0\) thì quỹ tích điểm M là đường tròn tâm G, bán kính \(r = \sqrt {\dfrac{{{k^2} - \left( {\dfrac{{A{B^2} + C{D^2}}}{2} + I{J^2}} \right)}}{4}} \).

Nếu \({k^2} = \left( {\dfrac{{A{B^2} + C{D^2}}}{2} + I{J^2}} \right)\) thì quỹ tích điểm M là một điểm G.

Nếu \({k^2} - \left( {\dfrac{{A{B^2} + C{D^2}}}{2} + I{J^2}} \right) < 0\) thì qỹ tích điểm M là tập rỗng.

Loigiaihay.com