Bài 6 trang 94 Tài liệu dạy – học Toán 9 tập 2

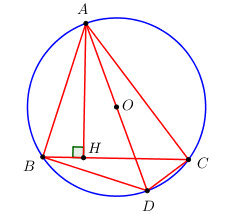
Đề bài

Cho tam giác ABC có ba cạnh a, b, c. Gọi S là diện tích và R là bán kính đường tròn ngoại tiếp, chứng minh công thức \(S = \dfrac{{abc}}{{4R}}\) .

Lời giải chi tiết

 

Đặt \(AB = c;\,\,AC = b;\,\,BC = a\). Vẽ đường kính AD và \(AH \bot BC\,\,\left( {H \in BC} \right)\).

Ta có \(\widehat {ACD}\) là góc nội tiếp chắn nửa đường tròn \( \Rightarrow \widehat {ACD} = {90^0}\).

Xét \(\Delta ABH\) và \(\Delta ADC\) có:

\(\widehat {AHB} = \widehat {ACD} = {90^0}\);

\(\widehat {ABH} = \widehat {ADC}\) (hai góc nội tiếp cùng chắn cung AC);

\( \Rightarrow \Delta ABH \sim \Delta ADC\,\,\left( {g.g} \right) \)

\(\Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{AB}}{{AD}}\)

\(\Rightarrow AH = \dfrac{{AB.AC}}{{AD}} = \dfrac{{bc}}{{2R}}\)

Khi đó ta có: \({S_{\Delta ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}\dfrac{{bc}}{{2R}}.a = \dfrac{{abc}}{{4R}}\) (đpcm).

 Loigiaihay.com