Bài 6 trang 62 SGK Đại số 10Giải các phương trình. Quảng cáo
Video hướng dẫn giải Giải các phương trình. LG a \(|3x – 2| = 2x + 3\); Phương pháp giải: Phương trình \(\left| {f\left( x \right)} \right| = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l} Lời giải chi tiết: Bình phương hai vế ta được: \(\begin{array}{l} Vậy phương trình có tập nghiệm \(S = \left\{ {5; - \dfrac{1}{5}} \right\}\) Cách khác: |3x – 2| = 2x + 3 (1) Tập xác định: D = R. + Nếu \(3x - 2 \ge 0 \Leftrightarrow x \ge \dfrac{2}{3}\) thì \(\left| {3x - 2} \right| = 3x - 2\) Phương trình (1) trở thành 3x – 2 = 2x + 3 \(\begin{array}{l} \Leftrightarrow 3x - 2x = 3 + 2\\ \Leftrightarrow x = 5\left( {TM} \right)\end{array}\) + Nếu \(3x - 2 < 0 \Leftrightarrow x < \dfrac{2}{3}\) thì \(\left| {3x - 2} \right| = - \left( {3x - 2} \right) = - 3x + 2\) Phương trình (1) trở thành \(\begin{array}{l} - 3x + 2 = 2x + 3\\ \Leftrightarrow - 3x - 2x = 3 - 2\\ \Leftrightarrow - 5x = 1\\ \Leftrightarrow x = - \dfrac{1}{5}\left( {TM} \right)\end{array}\) Vậy phương trình có hai nghiệm \({x_1} = 5\) và \({x_2} = - \dfrac{1}{5}\) LG b \(|2x -1| = |-5x – 2|\); Phương pháp giải: Bình phương hai vế. Lời giải chi tiết: Bình phương hai vế ta được:
Vậy phương trình có hai nghiệm \({x_1} = - 1,{x_2} = - \dfrac{1}{7}\) Cách 2: Bình phương hai vế ta được: \(\begin{array}{l} Cách 3: Sử dụng lý thuyết: \(\left| A \right| = \left| B \right| \Leftrightarrow \left[ \begin{array}{l} \(\begin{array}{l} LG c \(\dfrac{x-1}{2x -3}=\dfrac{-3x+1}{|x+1|}\) (3) Phương pháp giải: - Xét trường hợp của \(x\) để phá dấu giá trị tuyệt đối. - Giải phương trình có được và đối chiếu điều kiện đặt ra. Lời giải chi tiết: ĐKXĐ: \(\left\{ \begin{array}{l} + Xét x > –1, khi đó x + 1 > 0 nên |x + 1| = x + 1. Khi đó pt (3) \(\begin{array}{l} \Leftrightarrow \dfrac{{x - 1}}{{2x - 3}} = \dfrac{{ - 3x + 1}}{{x + 1}}\\ \Rightarrow \left( {x - 1} \right)\left( {x + 1} \right) \\= \left( { - 3x + 1} \right)\left( {2x - 3} \right)\\ \Leftrightarrow {x^2} - 1 = - 6{x^2} + 11x - 3\\ \Leftrightarrow 7{x^2} - 11x + 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{11 + \sqrt {65} }}{{14}}\left( {TM} \right)\\x = \dfrac{{11 - \sqrt {65} }}{{14}}\left( {TM} \right)\end{array} \right.\end{array}\) + Xét x < –1, khi đó x + 1 < 0 nên |x + 1| = –x – 1. Khi đó pt (3) \(\begin{array}{l} \Leftrightarrow \dfrac{{x - 1}}{{2x - 3}} = \dfrac{{ - 3x + 1}}{{ - x - 1}}\\ \Rightarrow \left( {x - 1} \right)\left( { - x - 1} \right) \\= \left( { - 3x + 1} \right)\left( {2x - 3} \right)\\ \Leftrightarrow - {x^2} + 1 = - 6{x^2} + 11x - 3\\ \Leftrightarrow 5{x^2} - 11x + 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{11 + \sqrt {41} }}{{10}}\left( {loai} \right)\\x = \dfrac{{11 - \sqrt {41} }}{{10}}\left( {loai} \right)\end{array} \right.\end{array}\) Vậy phương trình có hai nghiệm là \({x_{1,2}} = \dfrac{{11 \pm \sqrt {65} }}{{14}}\). LG d \(|2x + 5| = x^2+5x +1\). Phương pháp giải: - Xét trường hợp của \(x\) để phá dấu giá trị tuyệt đối. - Giải phương trình có được và đối chiếu điều kiện đặt ra. Lời giải chi tiết: +) Với \(2x + 5 \ge 0 \Leftrightarrow x ≥ -\dfrac{5}{2}\) ta có \(\left| {2x + 5} \right| = 2x + 5\) PT trở thành \(\eqalign{ +) Với \(2x + 5 < 0 \Leftrightarrow x < -\dfrac{5}{2}\) ta có \(\left| {2x + 5} \right| = -( 2x + 5) =-2x-5\) PT trở thành \(\eqalign{ Vậy phương trình đã cho có hai nghiệm \(x_1=1\) và \(x_2=-6\). Loigiaihay.com
|














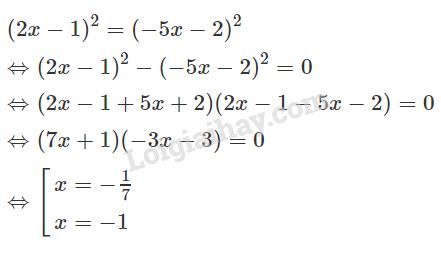






Danh sách bình luận