Bài 6 trang 140 SGK Đại số 10Trên đường tròn lượng giác gốc A, xác định các điểm M khác nhau Quảng cáo
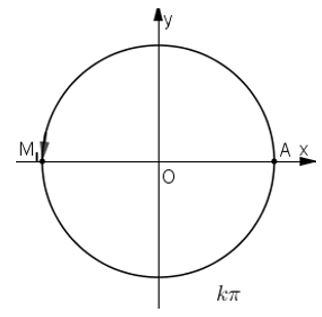
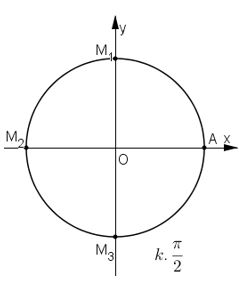
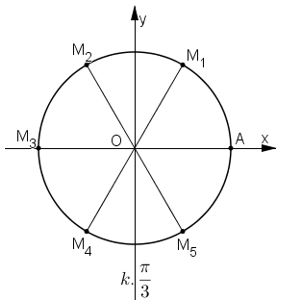
Video hướng dẫn giải Trên đường tròn lượng giác gốc \(A\), xác định các điểm \(M\) khác nhau, biết rằng cung \(AM\) có số đo tương ứng là (trong đó \(k\) là một số nguyên tuỳ ý) LG a \(kπ\); Phương pháp giải: +) Vẽ lên đường tròn lượng giác. Chú ý: Cung có số đo dạng \(\alpha + \frac{{k2\pi }}{n}\) thì sẽ có \(n\) điểm biểu diễn trên đường tròn lượng giác. Lời giải chi tiết: +) \(k = 0 \Rightarrow sdAM = 0\) \( \Rightarrow M \equiv A\left( {1;0} \right)\) +) \(k = 1 \Rightarrow sdAM = \pi \) \( \Rightarrow M \equiv {M_1}\left( { - 1;0} \right)\) Vậy ta có 2 điểm \(A,{M_1}\) như hình vẽ. Cách khác: Nếu k = 2n +1 (n ∈ Z) (thì kπ = (2n + 1)π = 2nπ + π nên M ≡ \(M_1(-1;0)\) Nếu k = 2n (n ∈ Z) thì kπ = 2nπ nên M ≡ A(1;0) Vậy ta có các điểm \(M_1(-1; 0), A(1; 0)\) LG b \(\displaystyle k{\pi \over 2}\); Phương pháp giải: +) Vẽ lên đường tròn lượng giác. Lời giải chi tiết: +) \(k = 0 \Rightarrow sdAM = 0\) \( \Rightarrow M \equiv A\left( {1;0} \right)\) +) \(k = 1 \Rightarrow sdAM = \dfrac{\pi }{2}\) \( \Rightarrow M \equiv {M_1}\left( {0;1} \right)\) +) \(k = 2 \Rightarrow sdAM = \dfrac{{2\pi }}{2} = \pi \) \( \Rightarrow M \equiv {M_2}\left( { - 1;0} \right)\) +) \(k = 3 \Rightarrow sdAM = \dfrac{{3\pi }}{2}\) \( \Rightarrow M \equiv {M_3}\left( {0; - 1} \right)\) Vậy ta có 4 điểm như hình vẽ. Cách khác: Nếu \(k = 4m\) thì \(k.\dfrac{\pi }{2} = 4m.\dfrac{\pi }{2}\) \( = 2m\pi \) \( \Rightarrow M \equiv A\left( {1;0} \right)\) Nếu \(k = 4m + 1\) thì \(k.\dfrac{\pi }{2} = \left( {4m + 1} \right).\dfrac{\pi }{2}\) \( = 2m\pi + \dfrac{\pi }{2}\) \( \Rightarrow M \equiv {M_1}\left( {0;1} \right)\) Nếu \(k = 4m + 2\) thì \(k.\dfrac{\pi }{2} = \left( {4m + 2} \right).\dfrac{\pi }{2}\) \( = 2m\pi + \pi \) \( \Rightarrow M \equiv {M_2}\left( { - 1;0} \right)\) Nếu \(k = 4m + 3\) thì \(k.\dfrac{\pi }{2} = \left( {4m + 3} \right).\dfrac{\pi }{2}\) \( = 2m\pi + \dfrac{{3\pi }}{2}\) \( \Rightarrow M \equiv {M_3}\left( {0; - 1} \right)\) LG c \(\displaystyle k{\pi \over 3}\). Phương pháp giải: +) Vẽ lên đường tròn lượng giác. Lời giải chi tiết: +) \(k = 0 \Rightarrow sdAM = 0\) \( \Rightarrow M \equiv A\left( {1;0} \right)\) +) \(k = 1 \Rightarrow sdAM = \dfrac{\pi }{3}\) \( \Rightarrow M \equiv {M_1}\left( {\dfrac{1}{2};\dfrac{{\sqrt 3 }}{2}} \right)\) +) \(k = 2 \Rightarrow sdAM = \dfrac{{2\pi }}{3}\) \( \Rightarrow M \equiv {M_2}\left( { - \dfrac{1}{2};\dfrac{{\sqrt 3 }}{2}} \right)\) +) \(k = 3 \Rightarrow sdAM = \dfrac{{3\pi }}{3} = \pi \) \( \Rightarrow M \equiv {M_3}\left( { - 1;0} \right)\) +) \(k = 4 \Rightarrow sdAM = \dfrac{{4\pi }}{3}\) \( \Rightarrow M \equiv {M_1}\left( { - \dfrac{1}{2}; - \dfrac{{\sqrt 3 }}{2}} \right)\) +) \(k = 5 \Rightarrow sdAM = \dfrac{{5\pi }}{3}\) \( \Rightarrow M \equiv {M_5}\left( {\dfrac{1}{2}; - \dfrac{{\sqrt 3 }}{2}} \right)\) Vậy ta có các điểm \(A,{M_1},{M_2},{M_3},{M_4},{M_5}\) như hình. Cách khác: Loigiaihay.com
|














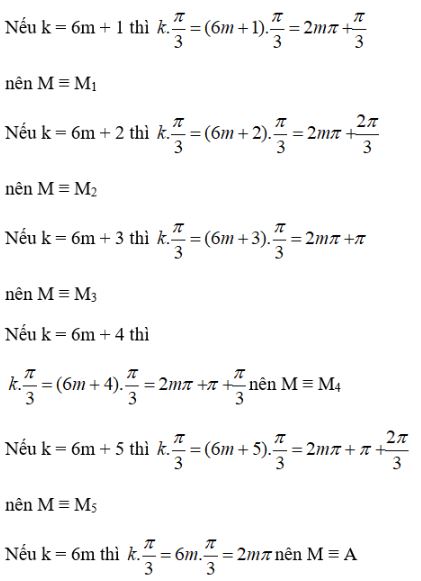






Danh sách bình luận