Bài 58 trang 109 SBT Hình học 10 Nâng cao

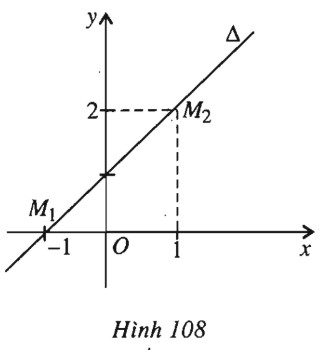
LG a

 Chứng minh rằng \((C_m)\) luôn là đường tròn với mọi giá trị của m.

Lời giải chi tiết:

Phương trình \((C_m)\) có dạng \({x^2} + {y^2} + 2ax + 2by + c = 0\).

Với \(a =  \dfrac{{m + 2}}{2} ,  b =  -  \dfrac{{m + 4}}{2} ,  c = m + 1\).

Ta có

\({a^2} + {b^2} - c\)

\(= {\left( { \dfrac{{m + 2}}{2}} \right)^2} + {\left( { \dfrac{{m + 4}}{2}} \right)^2} - (m + 1)\)

\(=  \dfrac{{{m^2} + 4m + 8}}{2} > 0\) với mọi \(m.\)

Vậy \((C_m)\) là đường tròn với mọi giá trị của \(m.\)

LG b

Tìm tập hợp tâm các đường tròn \((C_m)\) khi m thay đổi.

Lời giải chi tiết:

Tọa độ tâm \(I_m\) của đường tròn \((C_m)\) là \(\left\{ \begin{array}{l}x =  -  \dfrac{{m + 2}}{2}\\y =  \dfrac{{m + 4}}{2}\end{array} \right. \)

\(\Rightarrow    \left\{ \begin{array}{l}2x =  - (m + 2)\,\,\,\,\,\,\,\,\,\,(1)\\2y = m + 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\end{array} \right.\)

Cộng từng vế của (1) và (2), ta được \(2x+2y=2\) hay \(x+y-1=0.\)

Vậy tập hợp tâm của các đường tròn \((C_m)\) là đường thẳng có phương trình: \(x+y-1=0.\)

LG c

Chứng minh rằng khi \(m\) thay đổi, họ các đường tròn \((C_m)\) luôn đi qua hai điểm cố định.

Lời giải chi tiết:

Gọi \(M(x_0 ;y_0)\) là điểm cố định mà họ \((C_m)\) luôn đi qua. Khi đó ta có

\(\begin{array}{l}x_0^2 + y_0^2 + (m + 2){x_0} - (m + 4){y_0} + m + 1 = 0  \,\,\,\,\,\forall m\\ \Leftrightarrow    ({x_0} - {y_0} + 1)m + x_0^2 + y_0^2 + 2{x_0} - 4{y_0} + 1 = 0   \,\,\,\,\,\forall m\\ \Leftrightarrow    \left\{ \begin{array}{l}{x_0} - {y_0} + 1 = 0\,\,\,\,\,\,\,\,\,\,(1)\\x_0^2 + y_0^2 + 2{x_0} - 4{y_0} + 1 = 0 \,\,\,\,\,\,\,\,\,\,(2)\end{array} \right.\end{array}\)

Từ (1) suy ra \(x_0=y_0-1,\) thay vào (2), ta được:

\({({y_0} - 1)^2} + y_0^2 + 2({y_0} - 1) - 4{y_0} + 1 = 0\)

\(\Leftrightarrow       2y_0^2 - 4{y_0} = 0      \Leftrightarrow      \left[ \begin{array}{l}{y_0} = 0\\{y_0} = 2.\end{array} \right.\)

Với \(y_0=0\) thì \(x_0=-1\). Ta được điểm \(M_1(-1 ; 0).\)

Với \(y_0=2\) thì \(x_0=1.\) Ta được điểm \(M_1(1 ; 2).\)

Vậy họ đường tròn \((C_m)\) luôn đi qua hai điểm cố định là \(M_1(-1 ; 0)\) và \(M_2(1 ; 2).\)

LG d

Tìm những điểm trong mặt phẳng tọa độ mà họ \((C_m)\) không đi qua dù m lấy bất cứ giá trị nào.

Lời giải chi tiết:

(h.108).

\((C_m)\) không đi qua điểm \((x_1 ; y_1)\) với mọi \(m\) khi và chỉ khi phương trình (ẩn \(m\)) :

\(({x_1} - {y_1} + 1)m + x_1^2 + y_1^2 + 2{x_1} - 4{y_1} + 1 = 0\) vô nghiệm

\(\begin{array}{l} \Leftrightarrow    \left\{ \begin{array}{l}{x_1} - {y_1} + 1 = 0\\x_1^2 + y_1^2 + 2{x_1} - 4{y_1} + 1 \ne 0\end{array} \right.\\ \Leftrightarrow    \left\{ \begin{array}{l}{y_1} = {x_1} + 1\\{x_1} \ne  \pm 1.\end{array} \right.\end{array}\)

Vậy tập hợp các điểm trong mặt phẳng tọa độ mà họ \((C_m)\) không bao giờ đi qua với mọi giá trị của \(m\) là đường thẳng \(\Delta \) có phương trình \(y=x+1\), bỏ đi hai điểm \(M_1(-1 ; 0)\) và \(M_2(1 ; 2).\)

Loigiaihay.com