Bài 56 trang 89 SGK Toán 9 tập 2Xem hình 47. Hãy tìm số đo các góc của tứ giác ABCD Tổng hợp đề thi vào 10 tất cả các tỉnh thành trên toàn quốc Toán - Văn - Anh Quảng cáo
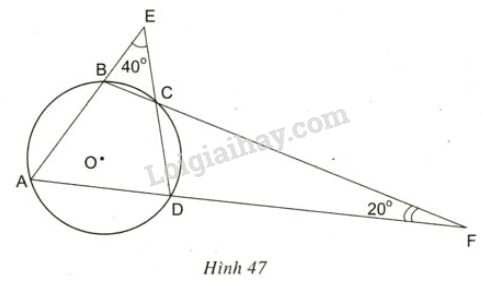
Đề bài Xem hình 47. Hãy tìm số đo các góc của tứ giác \(ABCD.\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Áp dụng công thức góc ngoài của tam giác. +) Tổng số đo hai góc đối diện của tứ giác nội tiếp bằng \(180^0.\) Lời giải chi tiết Ta có \(\widehat{BCE} = \widehat{DCF}\) (hai góc đối đỉnh) Đặt \(x = \widehat{BCE} = \widehat{DCF}\). Theo tính chất góc ngoài tam giác, ta có: \(\widehat{ABC}= x+40^0\) (góc ngoài của \(\Delta BCE\).) (1) \(\widehat{ADC}=x +20^0\) (góc ngoài của \(\Delta DCF\).) (2) Lại có \(\widehat{ABC} +\widehat{ADC}=180^0.\) (hai góc đối diện tứ giác nội tiếp). (3) Từ (1), (2), (3) suy ra: \(180^0 =2x + 60^0 \Rightarrow x = 60^0.\) Hay \( \widehat{BCE} = \widehat{DCF}=60^0. \) Từ (1), ta có: \(\widehat{ABC}=60^0 +40^0 =100^0.\) Từ (2), ta có: \(\widehat{ADC} = 60^0+20^0 = 80^0.\) \(\widehat{BCD}= 180^0 – \widehat{BCE} \) (hai góc kề bù) \(\Rightarrow\widehat{BCD} = 120^0\) \(\widehat{BAD} = 180^0 - \widehat{BCD}\) (hai góc đối diện của tứ giác nội tiếp) \(\Rightarrow \widehat{BAD}= 180^0– 120^0= 60^0.\) loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
|
