Bài 53 trang 127 Sách bài tập Hình học lớp 12 Nâng cao

Đề bài

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng h. Gọi I là trung điểm của cạnh bên SC. Tính khoảng cách từ điểm S đến mặt phẳng (ABI).

Lời giải chi tiết

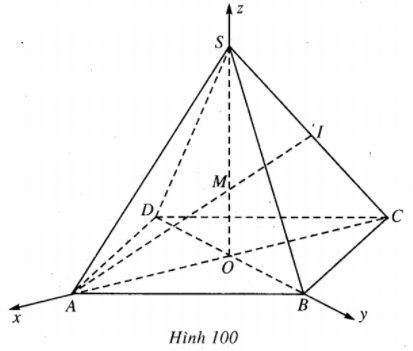
Ta chọn hệ trục Oxyz sao cho gốc tọa độ là tâm O của đáy, tia Ox chứa OA, tia Oy chứa OB, tia Oz chứa OS.

Khi đó :

\(\eqalign{  & A = \left( {{{a\sqrt 2 } \over 2};0;0} \right),  \cr  & B = \left( {0;{{a\sqrt 2 } \over 2};0} \right)  \cr  & C = \left( { - {{a\sqrt 2 } \over 2};0;0} \right),  \cr  & S = (0;0;h) \cr} \)

Rõ ràng giao điểm M của SO và AI chính là trọng tâm tam giác SAC nên

\(M\left( {0;0;{h \over 3}} \right)\)

Mặt phẳng (ABI) cũng chính là mặt phẳng (ABM). Vậy \(mp\left( {ABI} \right)\) có phương trình là :

\({x \over {{{a\sqrt 2 } \over 2}}} + {y \over {{{a\sqrt 2 } \over 2}}} + {z \over {{h \over 3}}} = 1.\)

Do đó, khoảng cách từ S tới mặt phẳng (ABI) là :

\(d = {{\left| {{h \over {{h \over 3}}} - 1} \right|} \over {\sqrt {{{\left( {{1 \over {{{a\sqrt 2 } \over 2}}}} \right)}^2} + {{\left( {{1 \over {{{a\sqrt 2 } \over 2}}}} \right)}^2} + {{\left( {{1 \over {{h \over 3}}}} \right)}^2}} }} = {2 \over {\sqrt {{2 \over {{a^2}}} + {2 \over {{a^2}}} + {9 \over {{h^2}}}} }} \)

\(\Rightarrow d = {{2ah} \over {\sqrt {4{h^2} + 9{a^2}} }}.\)

Loigiaihay.com