Bài 5 trang 69 SGK Toán 9 tập 2

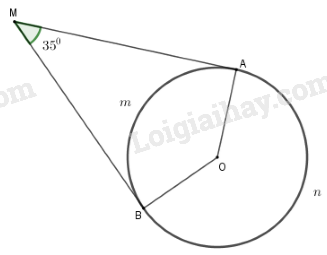
Đề bài

 Hai tiếp tuyến của đường tròn \((O)\) tại \(A\) và \(B\) cắt nhau tại \(M\). Biết \(\widehat{AMB}=35^0\).

a) Tính số đo của góc ở tâm tạo bởi hai bán kính \(OA, OB\).

b) Tính số đo mỗi cung \(AB\) (cung lớn và cung nhỏ).

Lời giải chi tiết

 

a) Vì \(MA,MB\) là hai tiếp tuyến của \(\left( O \right)\) cắt nhau tại \(M\) nên \(\widehat {OAM} = 90^\circ ;\,\widehat {MBO} = 90^\circ \) 

Xét tứ giác \(OBMA\) có \(\widehat {OAM} + \widehat {OBM} + \widehat {AMB} + \widehat {AOB} = 360^\circ \) (định lý tổng các góc của tứ giác)

Hay \(90^\circ  + 90^\circ  + 35^\circ  + \widehat {AOB} = 360^\circ \\ \Rightarrow \widehat {AOB} = 145^\circ .\)

Vậy số đo của góc ở tâm tạo bởi hai bán kính \(OA, OB\) là:\( \widehat {AOB} =145^0\)

b) Từ \(\widehat {AOB} = {145^0}\). \(\Rightarrow\) Số đo cung nhỏ \(\overparen{AB}\) là \(145^0\) và số đo cung lớn \(\overparen{AB}\) là: \({360^0} - {145^0} = {215^0}\)