Bài 4.21 trang 114 SGK Toán 11 tập 1 - Cùng khám pháCho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: Quảng cáo
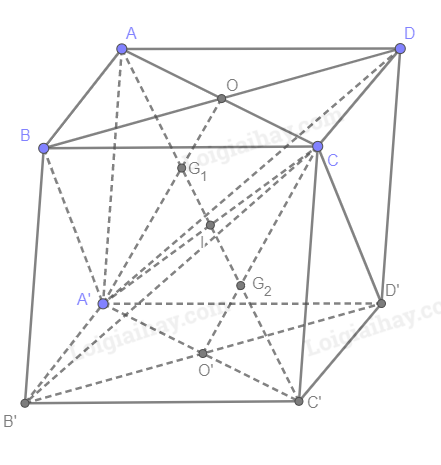
Đề bài Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: a) Hai mặt phẳng (BDA') và (B'D'C) song song với nhau. b) Đường chéo AC' đi qua các trọng tâm G1 và G2 của hai tam giác BDA' và B'D'C. c) G1 và G2 chia đoạn AC' thành ba phần bằng nhau. Phương pháp giải - Xem chi tiết a) Nếu mặt phẳng (P) chứa 2 đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q). b) Trọng tâm là giao điểm của các đường trung tuyến. c) Khoảng cách từ trọng tâm đến mỗi đỉnh bằng 2/3 đường trung tuyến tương ứng của đỉnh đó. Lời giải chi tiết
a) Ta có: BB' // DD' (cùng // CC') và BB' = DD' (cùng = CC') nên BB'D'D là hình bình hành Suy ra BD // B'D'. Nên BD // (B'D'C) (1) BC // A'D' (cùng // AD) và BC = A'D' (cùng = AD) nên BCD'A' là hình bình hành Suy ra A'B // CD'. Nên A'B // (B'D'C) (2) Từ (1) và (2) suy ra (BDA') song song với (B'D'C) b) Gọi O, O' lần lượt là giao điểm của AC và BD, A'C' và B'D'. Suy ra O, O' là trung điểm của AC, A'C' Gọi I là giao điểm của AC' và A'C AA' // CC' (cùng // BB') và AA' = CC' (cùng = BB') nên ACC'A' là hình bình hành. Suy ra I là trung điểm của AC' và A'C Nên AI và A'O là trung tuyến của tam giác AA'C Mà G1 là trọng tâm tam giác BDA'. Suy ra G1 là giao điểm của AI và A'O Tương tự, G2 là giao điểm của CO' và C'I G1 thuộc AI, G2 thuộc CI nên G1 và G2 đều thuộc AC'. c) G1 và G2 là trọng tâm của hai tam giác BDA' và B'D'C nên \(A{G_1} = \frac{2}{3}AI,{G_1}I = \frac{1}{3}AI\) và \(C'{G_2} = \frac{2}{3}C'I,{G_2}I = \frac{1}{3}CI\) Ta có: \({G_1}I + {G_2}I = \frac{1}{3}AI + \frac{1}{3}CI = \frac{1}{3}AI + \frac{1}{3}AI = \frac{2}{3}AI\) Suy ra AG1 = G1G2 = C'G2 (cùng = \(\frac{2}{3}AI\)) Vậy G1 và G2 chia đoạn AC' thành ba phần bằng nhau.
|




















Danh sách bình luận