Bài 42 Trang 175 SGK Đại số và Giải tích 12 Nâng caotìm nguyên hàm của các hàm số sau Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
LG a \(y = {1 \over {{x^2}}}\cos \left( {{1 \over x} - 1} \right)\); Phương pháp giải: Đổi biến \(u = {1 \over x} - 1\) Lời giải chi tiết: Đặt \(u = {1 \over x} - 1 \Rightarrow du = - {1 \over {{x^2}}}dx \) \(\Rightarrow {{dx} \over {{x^2}}} = - du\) Cách 2: Đưa vào vi phân LG b \(y = {x^3}{\left( {1 + {x^4}} \right)^3}\); Phương pháp giải: Đổi biến \(u=1+x^4\) Lời giải chi tiết: Đặt \(u = 1 + {x^4} \Rightarrow du = 4{x^3}dx \) \(\Rightarrow {x^3}dx = {{du} \over 4}\) \(\int {{x^3}{{\left( {1 + {x^4}} \right)}^3}dx}= {1 \over 4}\int {{u^3}du} \) \(= {{{u^4}} \over {16}} + C \) \(= {1 \over {16}} {\left( {1 + {x^4}} \right)^4} + C\) Cách 2: Đưa vào vi phân LG c \(y = {{x{e^{2x}}} \over 3}\); Phương pháp giải: Sử dụng phương pháp từng phần tính nguyên hàm: Đặt \(\left\{ \matrix{u = {x \over 3} \hfill \cr dv = {e^{2x}}dx \hfill \cr} \right. \) Lời giải chi tiết: Đặt \(\left\{ \matrix{ Suy ra: \(\int {{{x{e^{2x}}} \over 3}}dx \) \(= {1 \over 6}x{e^{2x}} - {1 \over 6}\int {{e^{2x}}dx} \) \(= {1 \over 6}x{e^{2x}} - {1 \over {12}}{e^{2x}} + C \) LG d \(y = {x^2}{e^x}\). Phương pháp giải: Đặt \(\left\{ \matrix{ Lời giải chi tiết: Đặt \(\left\{ \matrix{ Suy ra \(\int {{x^2}{e^x}dx = {x^2}{e^x} - 2\int {x{e^x}dx} } \) (1) Đặt \(\left\{ \matrix{ Do đó: \(\int {x{e^x}dx }\) \(= x{e^x} - \int {{e^x}dx}\) \( = x{e^x} - {e^x} + C_1 \) Từ (1) suy ra \(\int {{x^2}{e^x}dx} = {x^2}{e^x} - 2x{e^x} + 2{e^x} + C \) \(= {e^x}\left( {{x^2} - 2x + 2} \right) + C\) Loigiaihay.com
|














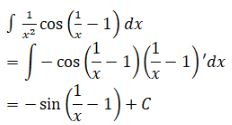
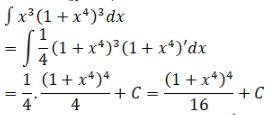






Danh sách bình luận