Bài 41 trang 129 SGK Toán 9 tập 2a) Chứng minh AOC và BDO là hai tam giác đồng dạng; từ đó suy ra tích AC.BD không đổi. Quảng cáo
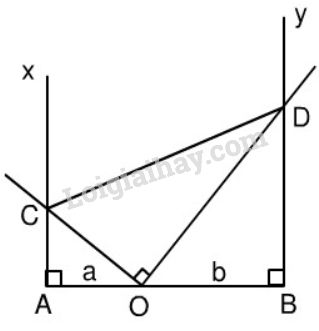
Đề bài Cho ba điểm \(A, O, B\) thẳng hàng theo thứ tự đó, \(OA = a, OB = b\) (\(a,b\) cùng đơn vị: cm). Qua \(A\) và \(B\) vẽ theo thứ tự các tia \(Ax\) và \(By\) cùng vuông góc với \(AB\) và cùng phía với \(AB\). Qua \(O\) vẽ hai tia vuông gaóc với nhau và cắt \(Ax\) ở \(C\), \(By\) ở \(D\) (xem hình 116). a) Chứng minh \(AOC\) và \(BDO\) là hai tam giác đồng dạng; từ đó suy ra tích \(AC.BD\) không đổi. b) Tính diện tích hình thang \(ABDC\) khi \(\widehat {COA} = {60^0}\) c) Với \(\widehat {COA} = {60^0}\) cho hình vẽ quay xung quanh \(AB\). Hãy tính tỉ số tích các hình do các tam giác \(AOC\) và \(BOD\) tạo thành
Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Hai tam giác có hai cặp góc tương ứng bằng nhau thì hai tam giác đó đồng dạng. b) Công thức tính diện tích hình thang có đáy lớn là \(a,\) đáy nhỏ là \(b\) và chiều cao \(h\) là: \(S = \dfrac{{\left( {a + b} \right)h}}{2}.\) c) Thể tích hình nón: \( V = \dfrac{1}{3}\pi {r^2}h.\) Lời giải chi tiết a) Xét hai tam giác vuông \(AOC\) và \(BDO\) ta có: \(\widehat A = \widehat B = {90^0}\) \(\widehat {AOC} = \widehat {B{\rm{D}}O}\) (cùng phụ với \(\widehat{BOD}\)). Vậy \(∆AOC\) đồng dạng \(∆BDO \, \, (g-g).\) \( \displaystyle \Rightarrow {{AC} \over {AO}} = {{BO} \over {B{\rm{D}}}}\) (2 cặp cạnh tương ứng tỉ lệ) \( \displaystyle\Rightarrow {{AC} \over a} = {b \over {B{\rm{D}}}}\) (1) Vậy \(AC . BD = a . b \) không đổi. b) Khi \(\widehat {COA} = 60^\circ \) , xét tam giác vuông \(ACO\) ta có \(\tan \widehat {AOC} = \dfrac{{AC}}{{OA}} \Rightarrow \tan 60^\circ = \dfrac{{AC}}{a} \Rightarrow AC = a\sqrt 3 \) mà \(AC.BD = ab\) (câu a) nên \(a\sqrt 3 .BD = ab \Rightarrow BD = \dfrac{{b\sqrt 3 }}{3}\) Ta có công thức tính diện tích hình thang \(ABCD\) là: \(\eqalign{ c) Theo đề bài ta có: Tam giác \(AOC\) khi quay quanh cạnh \(AB\) tạo thành hình nón có chiều cao \(OA = a\) và bán kính đáy \(AC = a\sqrt 3 \) nên thể tích hình nón là \({V_1} = \dfrac{1}{3}\pi .OA.A{C^2} = \dfrac{1}{3}\pi .a.{\left( {a\sqrt 3 } \right)^2} = \pi {a^3}\left( {c{m^3}} \right)\) Tam giác \(BOD\) khi quay quanh cạnh \(AB\) tạo thành hình nón có chiều cao \(OB = b\) và bán kính đáy \(BD = \dfrac{{b\sqrt 3 }}{3}\) nên thể tích hình nón là \({V_2} = \dfrac{1}{3}\pi .OB.B{D^2} = \dfrac{1}{3}\pi .b.{\left( {\dfrac{{b\sqrt 3 }}{3}} \right)^2} = \dfrac{{\pi {b^3}}}{9}\left( {c{m^3}} \right)\) Do đó \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\pi {a^3}}}{{\dfrac{{\pi {b^3}}}{9}}} = \dfrac{{9{a^3}}}{{{b^3}}}\) Loigiaihay.com
|




















Danh sách bình luận