Bài 4 trang 132 SGK Toán 8 tập 2

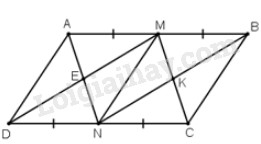
Đề bài

Cho hình bình hành $ABCD$. Các điểm $M, N$ theo thứ tự là trung điểm của $AB, CD$. Gọi $E$ là giao điểm của $AN$ và $DM$, $K$ là giao điểm của $BN$ và $CM$. Hình bình hành $ABCD$ phải có điều kiện gì để tứ giác $MENK$ là:

a) Hình thoi?

b) Hình chữ nhật?

c) Hình vuông?

Lời giải chi tiết

Vì $AB = 2MB, DC = 2DN$ (tính chất trung điểm)  

Mà $AB = DC$ (tính chất hình bình hành)

$\Rightarrow MB = DN$

Mà $MB // DN$

Tứ giác $MBND$ là hình bình hành (dấu hiệu nhận biết hình bình hành)

Suy ra: $MD=NB$ (tính chất)

Ta có: $AM=MB=DN=NC=\dfrac{DC}{2}$ và $AM//DN;MB//NC$

Nên các tứ giác $AMND, MBCN$ là hình bình hành. 

$\Rightarrow$ $E$ là trung điểm của $DM, K$ là trung điểm của $BN$ (tính chất hình bình hành)

$\Rightarrow$ $EM = NK$ (vì $DM=NB$)

Mà $EM // NK$ (do $DM // BN$)

$\Rightarrow$ $MENK$ là hình bình hành.

a) Để $MENK$ là hình thoi thì hình bình hành $MENK$ phải có hai đường chéo vuông góc. Tức là $MN ⊥ EK$.

Mà $MN//BC;\,EK//CD$

Suy ra $BC ⊥ CD$.

Vậy $ABCD$ phải là hình chữ nhật.

b) Để $MENK$ là hình chữ nhật thì hình bình hành $MENK$ phải có hai đường chéo bằng nhau. Tức là $MN = EK$.

Mà $MN = BC$, $EK = \dfrac{1}{2}CD$  suy ra:

$BC = \dfrac{1}{2}CD$.

c) Để $MENK$ là hình vuông thì $MENK$ phải vừa là hình thoi vừa là hình chữ nhật. Tức là hình bình hành $ABCD$ phải là hình chữ nhật có: $BC = \dfrac{1}{2}DC$

Loigiaihay.com