Bài 36 trang 123 SGK Toán 9 tập 1

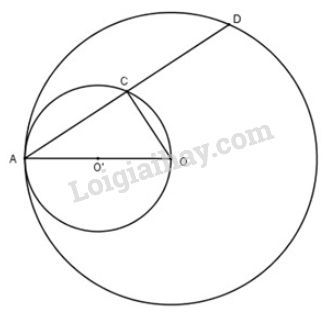
Đề bài

Cho đường tròn tâm $O$ bán kính $OA$ và đường tròn đường kính $OA$.

a) Hãy xác định vị trí tương đối của hai đường tròn.

b) Dây $AD$ của đường tròn lớn cắt đường tròn nhỏ ở $C$. Chứng minh rằng $AC=CD$.

Lời giải chi tiết

a) Gọi $O'$ là tâm của đường tròn đường kính $OA$.

Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O'. Độ dài $OO'=d$. 

Vì $O'$ là tâm của đường tròn đường kính $OA$ nên $r=O'A=O'O=\dfrac{OA}2.$

Vì điểm O' nằm giữa hai điểm O và A nên $AO'+OO'=OA$

$\Rightarrow OO'=OA-O'A$ hay $d=R-r$ 

$\Rightarrow$ Đường tròn $(O)$ và đường tròn $(O')$ tiếp xúc trong. 

b) Xét tam giác ACO có trung tuyến CO' = $\dfrac{1}{2}.AO(=r)$ nên $\Delta CAO$ vuông tại $C$

$\Rightarrow OC\perp AD$ tại C.

Cách 1:

Xét đường tròn (O) có OC là một phần đường kính và AD là dây của đường tròn mà $OC \bot AD$ tại C (cmt) $\Rightarrow CA=CD$ (đường kính vuông góc với một dây thì đi qua trung điểm dây đó).

Cách 2:

Xét hai tam giác vuông ACO và DCO, có:

$AO = OD (=R)$

CO chung

$\Rightarrow \Delta ACO = \Delta DCO$(cạnh huyền - cạnh góc vuông)

$\Rightarrow AC = DC$ (2 cạnh tương ứng)

Cách 3:

Vì OA = OD(=R) nên tam giác OAD cân tại O

$\Rightarrow$ Đường cao OC đồng thời là đường trung tuyến

$\Rightarrow$ C là trung điểm của AD

$\Rightarrow$ CA = CD