Bài 32 trang 126 SGK Đại số 10 nâng caoLập bảng xét dấu của các biểu thức Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
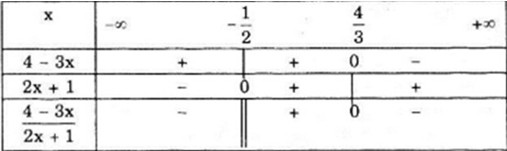
Lập bảng xét dấu của các biểu thức LG a \({{4 - 3x} \over {2x + 1}}\) Phương pháp giải: - Biến đổi biểu thức về tích, thương các nhị thức bậc nhất. - Tìm nghiệm của các nhị thức bậc nhất trên. - Sắp xếp các nghiệm theo thứ tự tăng dần và xét dấu theo chú ý "phải cùng trái khác". - Từ đó suy ra dấu của biểu thức đã cho. Lời giải chi tiết: Ta có: \(4 - 3x = 0 \Leftrightarrow x = \dfrac{4}{3};\) \(2x + 1 = 0 \Leftrightarrow x = - \dfrac{1}{2}\) Bảng xét dấu:
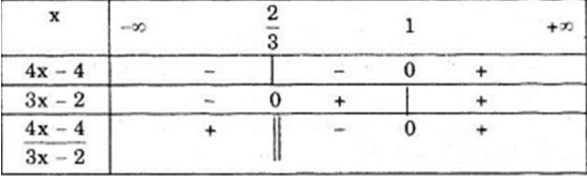
LG b \(1 - {{2 - x} \over {3x - 2}}\) Lời giải chi tiết: Ta có: \(1 - \frac{{2 - x}}{{3x - 2}} = \frac{{3x - 2 - 2 + x}}{{3x - 2}} = \frac{{4x - 4}}{{3x - 2}}\) \(4x - 4 = 0 \Leftrightarrow x = 1;\) \(3x - 2 = 0 \Leftrightarrow x = \frac{2}{3}\) Ta có bảng xét dấu:
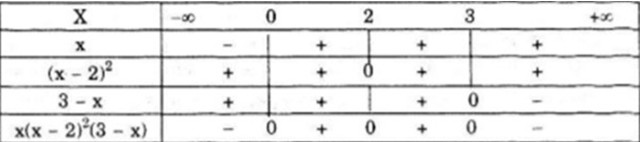
LG c \(x{(x - 2)^2}(3 - x)\) Lời giải chi tiết: \(x - 2 = 0 \Leftrightarrow x = 2;\) \(3 - x = 0 \Leftrightarrow x = 3\) Ta có bảng xét dấu sau:
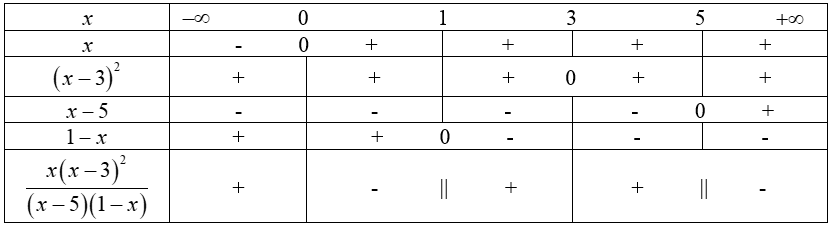
LG d \({{x{{(x - 3)}^2}} \over {(x - 5)(1 - x)}}\) Lời giải chi tiết: Ta có: \(x - 3 = 0 \Leftrightarrow x = 3;\) \(x - 5 = 0 \Leftrightarrow x = 5;\) \( 1 - x = 0 \Leftrightarrow x = 1\) Ta có bảng xét dấu sau:
Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
