Bài 37 trang 127 SGK Đại số 10 nâng cao

LG a

\(( - \sqrt 3 x + 2)(x + 1)(4x - 5) > 0\)

Phương pháp giải:

- Tìm nghiệm các nhị thức bậc nhất và sắp xếp chúng theo thứ tự tăng dần.

- Lập bảng xét dấu suy ra tập nghiệm.

Lời giải chi tiết:

Ta có: 

\(\begin{array}{l}
- \sqrt 3 x + 2 = 0 \Leftrightarrow x = \frac{2}{{\sqrt 3 }}\\
x + 1 = 0 \Leftrightarrow x = - 1\\
4x - 5 = 0 \Leftrightarrow x = \frac{5}{4}
\end{array}\)

Bảng xét dấu:

Vậy \(S = ( - \infty , - 1) \cup ({2 \over {\sqrt 3 }};{5 \over 4})\)

LG b

\({{3 - 2x} \over {(3x - 1)(x - 4)}} < 0\)

Lời giải chi tiết:

Ta có: 

\(\begin{array}{l}
3 - 2x = 0 \Leftrightarrow x = \frac{3}{2}\\
3x - 1 = 0 \Leftrightarrow x = \frac{1}{3}\\
x - 4 = 0 \Leftrightarrow x = 4
\end{array}\)

Bảng xét dấu:

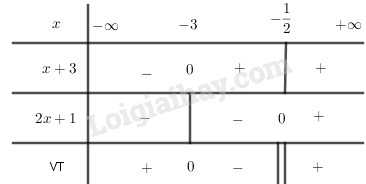
Vậy \(S = ({1 \over 3};{3 \over 2}) \cup (4, + \infty )\)

LG c

\({{ - 3x + 1} \over {2x + 1}} \le  - 2\)

Lời giải chi tiết:

Ta có:

\(\eqalign{
& {{ - 3x + 1} \over {2x + 1}} \le - 2 \cr & \Leftrightarrow \frac{{ - 3x + 1}}{{2x + 1}} + 2 \le 0\cr &\Leftrightarrow {{ - 3x + 1 + 2(2x + 1)} \over {2x + 1}} \le 0 \cr 
& \Leftrightarrow {{x + 3} \over {2x + 1}} \le 0 \cr} \)

Bảng xét dấu:

Từ bảng xét dấu ta thấy:  \(- 3 \le x < - {1 \over 2}\)

Vậy \(S = {\rm{[ - 3,}}-{1 \over 2})\)

LG d

\({{x + 2} \over {3x + 1}} \le {{x - 2} \over {2x - 1}}\)

Lời giải chi tiết:

Ta có:

\(\eqalign{
& {{x + 2} \over {3x + 1}} \le {{x - 2} \over {2x - 1}} \cr& \Leftrightarrow \frac{{x + 2}}{{3x + 1}} - \frac{{x - 2}}{{2x - 1}} \le 0\cr &\Leftrightarrow {{(x + 2)(2x - 1) - (x - 2)(3x + 1)} \over {(3x + 1)(2x - 1)}} \le 0 \cr 
& \Leftrightarrow \frac{{2{x^2} + 4x - x - 2 - \left( {3{x^2} - 6x + x - 2} \right)}}{{\left( {3x + 1} \right)\left( {2x - 1} \right)}} \le 0 \cr&\Leftrightarrow {{ - {x^2} + 8x} \over {(3x + 1)(2x - 1)}} \le 0\cr& \Leftrightarrow \frac{{{x^2} - 8x}}{{\left( {3x + 1} \right)\left( {2x - 1} \right)}} \ge 0\cr& \Leftrightarrow {{x(x - 8)} \over {(3x + 1)(2x - 1)}} \ge 0 \cr} \)

Lập bảng xét dấu vế trái

Vậy tập nghiệm của bất phương trình là:\(S = ( - \infty ; - {1 \over 3}) \cup {\rm{[}}0,{1 \over 2}) \cup {\rm{[}}8, + \infty )\)

Loigiaihay.com