Bài 3 trang 50 SGK Hình học 12

Đề bài

Chứng minh rằng hình chóp có tất cả các cạnh bên bằng nhau nội tiếp được trong một mặt cầu.

Lời giải chi tiết

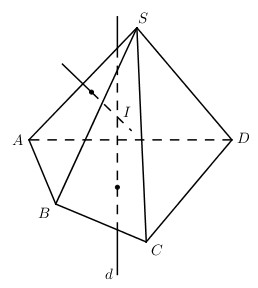
Giả sử ta có hình chóp \(S.{A_1}{A_2}{A_3}...{A_n}\) với \({A_1}{A_2}{A_3}...{A_n}\) là đa giác đáy.

Ta có: \(S{A_1} = S{A_2} = S{A_3} = ... = S{A_n}\)

Kẻ  \(SH\) vuông góc với mặt phẳng đáy. Dễ thấy: \(\Delta \;SH{A_1} = \Delta \;SH{A_2} = \Delta \;SH{A_3} = ... = \Delta \,SH{A_n}\) (cạnh huyền - cạnh góc vuông)

\( \Rightarrow H{A_1} = H{A_2} = H{A_3} = ... = H{A_n}\) 

\( \Rightarrow \) H là tâm đường tròn ngoại tiếp đa giác đáy \({A_1}{A_2}{A_3}...{A_n}\)

Xét tam giác \(\Delta \,SH{A_1}\), kẻ đường trung trực của cạnh \(S{A_1}\), đường này cắt \(SH\) ở điểm \(I\)

\(\Rightarrow IA = IS\).

Xét \(\Delta \;SI{A_1},\Delta \;SI{A_2},\Delta \;SI{A_3},...,\Delta \,SI{A_n}\) ta có:

\(\left. \begin{array}{l}
IS \text{ chung} \\
S{A_1} =S{A_2} = ... = \,S{A_n}\\
\widehat {SI{A_1}} =\widehat {SI{A_2}} = ... = \widehat {SI{A_n}}
\end{array} \right\}\)

\( \Rightarrow \Delta SI{A_1} = \Delta SI{A_2} = ... = \Delta SI{A_n}\)

\( \Rightarrow I{A_1} = \;I{A_2} = \;I{A_3} = ... = \,I{A_n} = IS\)

 hay điểm \(I\) cách đều các đỉnh của hình chóp, do đó \(I\) là tâm mặt cầu đi qua các đỉnh của hình chóp.

Loigiaihay.com