Bài 26 trang 118 SGK Toán 7 tập 1Xét bài toán: " Cho tam giác ABC, M là trung điểm của BC, Trên tia đối của MA lấy điểm E sao cho ME=MA. Chứng minh rẳng AB//CE'. Quảng cáo
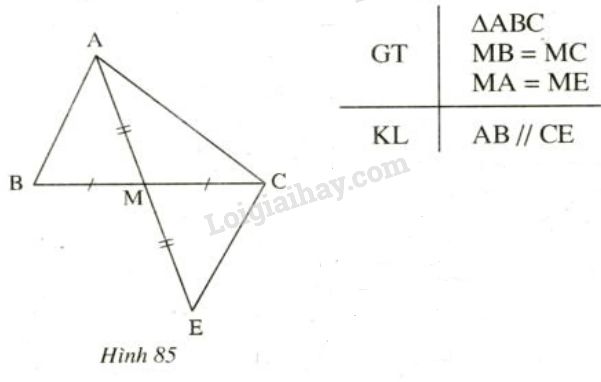
Đề bài Xét bài toán: " Cho tam giác \(ABC, M\) là trung điểm của \(BC.\) Trên tia đối của \(MA\) lấy điểm \( E\) sao cho \(ME=MA.\) Chứng minh rẳng \(AB//CE"\). Dưới đây là hình vẽ và giả thiết, kết luận của bài toán (h.85)
Hãy sắp xếp lại năm câu sau đây một cách hợp lí để giải bài toán trên: 1) \(MB = MC\) (giả thiết) \(\widehat{AMB}=\widehat{EMC}\) (hai góc đối đỉnh) \(MA= ME\) (giả thiết) 2) Do đó \(∆AMB=∆EMC\) (c.g.c) 3) \(\widehat{MAB}=\widehat{MEC}\) \( \Rightarrow AB//CE\) (có hai góc bằng nhau ở vị trí so le trong) 4) \(∆AMB= ∆EMC\) \( \Rightarrow \widehat{MAB}=\widehat{MEC}\) (hai góc tương ứng) 5) \(∆AMB\) và \( ∆EMC\) có: Video hướng dẫn giải Phương pháp giải - Xem chi tiết Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. Lời giải chi tiết Thứ tự sắp xếp là: \(5; 1; 2; 4; 3\) \(∆AMB\) và \( ∆EMC\) có: \(MB = MC\) (giả thiết) \(\widehat{AMB}=\widehat{EMC}\) (hai góc đối đỉnh) \(MA= ME\) (giả thiết) Do đó \(∆AMB=∆EMC\) (c.g.c) \(∆AMB= ∆EMC\) \( \Rightarrow \widehat{MAB}=\widehat{MEC}\) (hai góc tương ứng) \(\widehat{MAB}=\widehat{MEC}\) \( \Rightarrow AB//CE\) (có hai góc bằng nhau ở vị trí so le trong) Loigiaihay.com
|




















Danh sách bình luận