Bài 25 trang 66 SGK Hình học 10 nâng cao

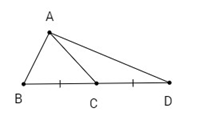
Đề bài

Tam giác \(ABC\) có \(a = 5,\,b = 4,\,c = 3\). Lấy điểm \(D\) đối xứng với \(B\) qua \(C\). Tính độ dài \(AD\).

Lời giải chi tiết

D đối xứng với B qua C nên C là trung điểm BD hay BD=2BC=2.5=10.

Áp dụng công thức tính trung tuyến \(AC\) trong tam giác \(ABD\) ta có

\(A{C^2} = {{A{B^2} + A{D^2}} \over 2} - {{B{D^2}} \over 4}\)

\( \Rightarrow \,\,{4^2} = {{{3^2} + A{D^2}} \over 2} - {{{{10}^2}} \over 4}\)

\( \Leftrightarrow 41 = \frac{{9 + A{D^2}}}{2} \Leftrightarrow 9 + A{D^2} = 82\)

\(\Rightarrow \,A{D^2} = 73\,\,\, \Rightarrow \,AD = \sqrt {73}  \approx 8,5.\)

Loigiaihay.com