Bài 25 trang 42 SBT Hình học 10 Nâng cao

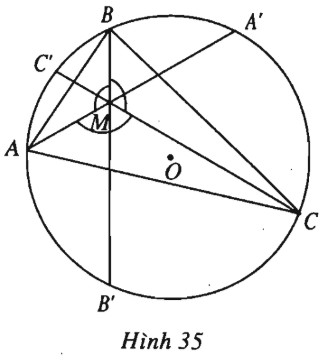
Đề bài

Cho tam giác \(ABC\) nội tiếp trong đường tròn \((O)\) và một điểm \(M\) sao cho các góc \(AMB, BMC, CMA\) đều bằng \(120^0\). Các đường thẳng \(AM, BM, CM\) cắt đường tròn \((O)\) lần lượt tại \(A’, B’, C’\). Chứng minh rằng:

\(MA+MB+MC\)\(=MA’+MB’+MC’.\)

Lời giải chi tiết

(h.35).

Lấy các điểm \(A_1, B_1, C_1\) sao cho \(\overrightarrow {M{A_1}}  = \dfrac{{\overrightarrow {MA} }}{{MA}};\)  \(  \overrightarrow {M{B_1}}  = \dfrac{{\overrightarrow {MB} }}{{MB}};\) \(\overrightarrow {M{C_1}}  = \dfrac{{\overrightarrow {MC} }}{{MC}} \), khi đó cả ba vec tơ trên đều có độ  dài bằng 1, mà góc giữa hai vectơ bất kì trong chúng đều bằng \(120^0\) nên \(M\) là tâm của tam giác đều \(A_1 B_1 C_1\).

Theo bài 24, ta có

\(2\overrightarrow {MA} .\overrightarrow {MO}\)

\(  = MA(MA - MA')\), suy ra \(2\dfrac{{\overrightarrow {MA} }}{{MA}}.\overrightarrow {MO} \)

\(= MA - MA'\),

hay \(2\overrightarrow {M{A_1}} .\overrightarrow {MO}  = MA - MA'\).

Tương tự

\(2\overrightarrow {M{B_1}} .\overrightarrow {MO}  = MB - MB',\)  \( 2\overrightarrow {M{C_1}} .\overrightarrow {MO}  = MC - MC'.\)

Từ đó ta có

\(MA + MB + MC\)\( - MA' - MB' - MC' \)

\(= 2(\overrightarrow {M{A_1}}  + \overrightarrow {M{B_1}}  + \overrightarrow {M{C_1}} ).\overrightarrow {MO}  = 0\)

Hay

\(MA + MB + MC\)\( = MA' + MB' + MC'\)

Loigiaihay.com