Bài 23 trang 65 SGK Hình học 10 nâng cao

Đề bài

Gọi \(H\) là trực tâm của tam giác không vuông \(ABC\). Chứng minh rằng bán kính các đường tròn ngoại tiếp các tam giác \(ABC,\,HBC,\,HCA,\,HAB\) bằng nhau.

Lời giải chi tiết

Trường  hợp 1: Tam giác \(ABC\) có ba góc nhọn.

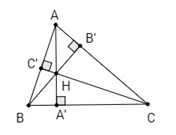
Gọi \(R,\,{R_1}\) lần lượt là bán kính đường tròn ngoại tiếp tam giác \(ABC, HBC\).

Áp dụng định lí sin ta có

\({{BC} \over {\sin A}} = 2R\,;\,\,{{BC} \over {\sin \widehat {BHC}}} = 2{R_1}\)

Xét tứ giác AB'HC' có: \(\widehat {B'} + \widehat {C'} = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp.

\( \Rightarrow \widehat A + \widehat {B'HC'} = {180^0}\) (tính chất tứ giác nội tiếp)

Mà \(\widehat {BHC} + \widehat A = \widehat {{B'}H{C'}} + \widehat A = {180^0}\) (Vì \(\widehat {BHC}\) và \(\widehat {{B'}H{C'}}\) đối đỉnh)

\( \Rightarrow \,\,\sin A = \sin \widehat {BHC}\) (hai góc bù nhau thì sin bằng nhau)

Do đó \(\frac{{BC}}{{\sin A}} = \frac{{BC}}{{\sin \widehat {BHC}}}  \)\(\Rightarrow 2R = 2{R_1}\,\, \Rightarrow \,\,R = {R_1}.\)

Vậy bán kính đường tròn ngoại tiếp tam giác \(HBC\) bằng bán kính đường tròn ngoại tiếp tam giác \(ABC\).

Tương tự bán kính đường tròn ngoại tiếp tam giác \(HCA, HAB\) bằng bán kính đường tròn ngoại tiếp tam giác \(ABC\).

Trường hợp 2: Tam giác \(ABC\) có góc tù.

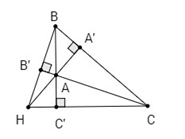
Áp dụng định lí sin ta có:

\({{BC} \over {\sin \widehat{BAC}}} = 2R\,;\,\,{{BC} \over {\sin \widehat {BHC}}} = 2{R_1}\)

Xét tứ giác AB'HC' có: \(\widehat {B'} + \widehat {C'} = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp.

\( \Rightarrow \widehat H + \widehat {B'AC'} = {180^0}\) (tính chất tứ giác nội tiếp)

Mà \(\widehat {B'AC'} = \widehat {BAC}\) (đối đỉnh) nên \(\widehat H + \widehat {BAC} = {180^0}\)

\( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BHC}\) (hai góc bù nhau thì sin bằng nhau)

\( \Rightarrow \frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{BC}}{{\sin \widehat {BHC}}} \)

\(\Rightarrow 2R = 2{R_1} \)\( \Rightarrow \,\,R = {R_1}\)

Tương tự  ta chứng minh được bán kính đường tròn ngoại tiếp tam giác \(HCA, HAB\) bằng bán kính đường tròn ngoại tiếp tam giác \(ABC\).

Loigiaihay.com