Bài 2 trang 77 SGK Hình học 11

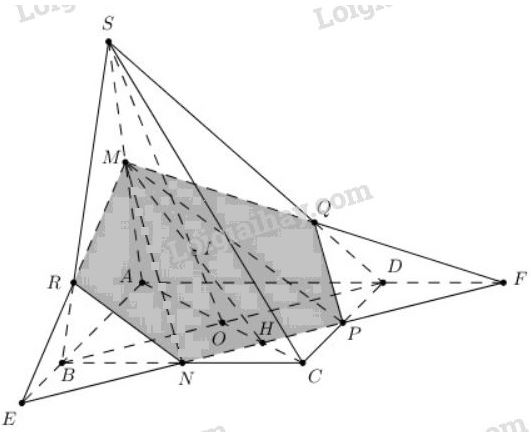
Đề bài

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M, N, P$ theo thứ tự là trung điểm của các đoạn thẳng $SA, BC, CD$. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng $(MNP)$.

Gọi $O$ là giao điểm hai đường chéo của hình bình hành $ABCD$, hãy tìm giao điểm của đường thẳng $SO$ với $mp (MNP)$.

Lời giải chi tiết

a) Trong mặt phẳng $(ABCD)$ kéo dài $NP$ cắt đường thẳng $AB, AD$ lần lượt tại $E, F$.

Trong mặt phẳng $(SAD)$ gọi $Q=SD\cap MF$

Trong mặt phẳng $(SAB)$ gọi $R=SB\cap ME$

Do đó 

$\Rightarrow \left\{ \begin{array}{l} \left( {MNP} \right) \cap \left( {SAD} \right) = MQ\\ \left( {MNP} \right) \cap \left( {SDC} \right) = QP\\ \left( {MNP} \right) \cap \left( {ABCD} \right) = PN\\ \left( {MNP} \right) \cap \left( {SBC} \right) = NR\\ \left( {MNP} \right) \cap \left( {SAB} \right) = RM \end{array} \right.$

Từ đó ta có thiết diện là ngũ giác $MQPNR$.

b) Trong $(ABCD)$ gọi $H=AC\cap NP$

$\Rightarrow H \in AC \subset \left( {SAC} \right)$$\Rightarrow MH \subset \left( {SAC} \right)$

Trong $\left( {SAC} \right)$, gọi $I = SO \cap MH \Rightarrow \left\{ \begin{array}{l}I \in SO\\I \in MH \subset \left( {MNP} \right)\end{array} \right.$

$\Rightarrow I = SO \cap \left( {MNP} \right)$.

Loigiaihay.com