Bài 2 trang 68 SGK Đại số 10Giải các hệ phương trình Quảng cáo
Video hướng dẫn giải Giải các hệ phương trình LG a \(\left\{\begin{matrix} 2x - 3y = 1 & \\ x + 2y = 3;& \end{matrix}\right.\) Phương pháp giải: Ta có thể giải hệ phương trình bằng phương pháp thế, hoặc phương pháp cộng đại số. Lời giải chi tiết: Giải bằng phương pháp thế: \(\left\{ \begin{array}{l} Từ (2) suy ra x = 3 – 2y, thế vào phương trình (1) ta được: 2.(3 – 2y) – 3y = 1 ⇔ 6 – 4y – 3y = 1 ⇔ 7y = 5 ⇔ y = 5/7. Thay y = 5/7 vào x = 3 – 2y ta được : x = 3 – 2.5/7 = 11/7. Vậy hệ phương trình có nghiệm (x ; y) = (11/7 ; 5/7). Kết luận: Hệ phương trình có nghiệm duy nhất (\(\dfrac{11}{7}\); \(\dfrac{5}{7}\)). Giải bằng phương pháp cộng đại số: \(\left\{ \begin{array}{l} \( \Leftrightarrow \left\{ \begin{array}{l} \( \Leftrightarrow \left\{ \begin{array}{l} LG b \(\left\{\begin{matrix} 3x + 4y = 5 & \\ 4x - 2y = 2;& \end{matrix}\right.\) Lời giải chi tiết: \(\left\{ \begin{array}{l} \( \Leftrightarrow \left\{ \begin{array}{l} \( \Leftrightarrow \left\{ \begin{array}{l} Đáp số: (\(\dfrac{9}{11}\); \(\dfrac{7}{11}\)). Cách khác: \(\left\{\begin{matrix} 3x + 4y = 5 \,\,(1)& \\ 4x - 2y = 2\,\,(2)& \end{matrix}\right.\) Ta có: \(\left( 2 \right) \Leftrightarrow 2x - y = 1 \Leftrightarrow y = 2x - 1\) Thế y=2x-1 vào phương trình (1) ta được 3x + 4.(2x – 1) = 5 ⇔ 3x + 8x – 4 = 5 ⇔ 11x = 9 ⇔ x = 9/11 Thay vào phương trình y = 2x – 1 ta được y = 2.9/11 – 1 = 7/11. Vậy hệ phương trình có nghiệm (x; y) = (9/11; 7/11) LG c \(\left\{\begin{matrix} \dfrac{2}{3}x +\dfrac{1}{2}y =\dfrac{2}{3}& \\ \dfrac{1}{3}x - \dfrac{3}{4}y= \dfrac{1}{2}& \end{matrix}\right.\) Lời giải chi tiết: Hệ đã cho \( \Leftrightarrow \) \(\left\{\begin{matrix} 4x + 3y = 4 & \\ 4x - 9y = 6& \end{matrix}\right.\) (Nhân cả hai vế của pt trên với 6, nhân cả hai vế của pt dưới với 12) \(\Leftrightarrow \left\{\begin{matrix} 4x + 3y = 4 & \\ 12y =-2\end{matrix}\right.\) (Lấy phương trình thứ nhất trừ đi phương trình thứ hai) \( \Leftrightarrow \left\{ \begin{array}{l} \( \Leftrightarrow \) \(\left\{\begin{matrix} x = \dfrac{9}{8} & \\ y =-\dfrac{1}{6}\end{matrix}\right.\). Cách khác:
Thay \(x = \frac{9}{8}\) vào \(y = \frac{4}{3}\left( {1 - x} \right) = \frac{4}{3}\left( {1 - \frac{9}{8}} \right) = - \frac{1}{6}\) Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {\frac{9}{8}; - \frac{1}{6}} \right)\). LG d \(\left\{\begin{matrix} 0,3x - 0,2y =0,5 & \\ 0,5x + 0,4y = 1,2.& \end{matrix}\right.\) Lời giải chi tiết: Hệ \( \Leftrightarrow \left\{\begin{matrix} 3x - 2y = 5 & \\ 5x + 4y = 12\end{matrix}\right.\) (Nhân mỗi phương trình với \(10\)) \( \Leftrightarrow \left\{ \begin{array}{l} Cách 2:
Cách 3: Hệ \( \Leftrightarrow \left\{\begin{matrix} 3x - 2y = 5 \,\,(1)& \\ 5x + 4y = 12\,\,(2)\end{matrix}\right.\) Từ (1) rút ra 2y = 3x – 5, thay vào phương trình (2) ta được: 5x + 2.(3x – 5) = 12 ⇔ 5x + 6x – 10 = 12 ⇔ 11x = 22 ⇔ x = 2. Thay x = 2 vào phương trình 2y = 3x – 5 ta được 2y = 1 ⇔ y = 1/2. Vậy hệ phương trình có nghiệm (x ; y) = (2 ; 1/2) Loigiaihay.com
|














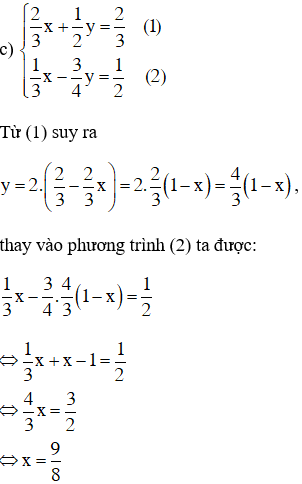
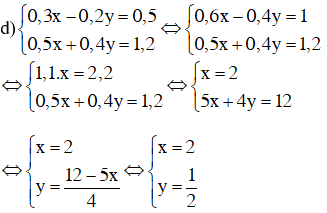






Danh sách bình luận