Bài 5 trang 68 SGK Đại số 10Giải các hệ phương trình Quảng cáo
Video hướng dẫn giải Giải các hệ phương trình LG a \(\left\{\begin{matrix} x + 3y + 2z =8 & \\ 2x + 2y + z =6& \\ 3x +y+z=6;& \end{matrix}\right.\) Phương pháp giải: Giải hệ phương trình bằng phương pháp thế hoặc đưa về dạng tam giác để giải. Lời giải chi tiết: Phương pháp thế: \(x + 3y + 2z = 8 \Rightarrow x = 8 - 3y - 2z\). Thế vào phương trình thứ hai và thứ ba thì được \( \Leftrightarrow \left\{\begin{matrix} x= 8 - 3y -2z & \\ 2(8-3y-2z)+2y +z=6& \\ 3(8-3y-2z) +y+z=6& \end{matrix}\right.\\ \Leftrightarrow \left\{\begin{matrix} x= 8 - 3y -2z & \\ 4y +3z=10& \\ 8y + 5z =18& \end{matrix}\right.\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x = 8 - 3y - 2z\\8y + 6z = 20\\8y + 5z = 18\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 8 - 3y - 2z\\z = 2\\8y + 5.2 = 18\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}x = 8 - 3y - 2z\\z = 2\\y = 1\end{array} \right.\end{array}\) \(\Leftrightarrow \left\{ \begin{array}{l} Nghiệm của hệ phương trình ban đầu là \((1; 1; 2)\). Chú ý: Ta có thể đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số như sau: Nhân cả hai phương trình dưới với 2 rồi trừ cho phương trình đầu ta được:
LG b \(\left\{\begin{matrix} x - 3y + 2z =-7 & \\ -2x + 4y + 3z =8& \\ 3x +y-z=5.& \end{matrix}\right.\) Phương pháp giải: Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số. Lời giải chi tiết: Rút x từ phương trình đầu tiên sau đó thay vào các phương trình còn lại của hệ. \(\begin{array}{l} Cách khác: Đưa hệ phương trình về hệ dạng tam giác bằng cách khử dần ẩn số. Nhân phương trình (1) với 2 rồi cộng với phương trình (2) và nhân phương trình (1) với 3 rồi trừ đi phương trình (3) ta được: \(\left\{ \begin{array}{l} \( \Leftrightarrow \left\{ \begin{array}{l} Loigiaihay.com
|














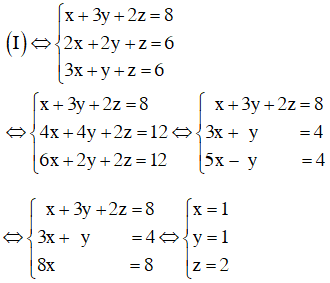






Danh sách bình luận