Bài 2 trang 131 SGK Toán 8 tập 2

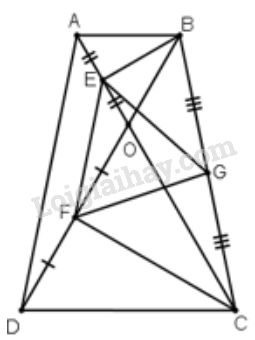
Đề bài

Cho hình thang $ABCD \;(AB // CD)$ có hai đường chéo cắt nhau ở $O$ và tam giác $ABO$ là tam giác đều. Gọi $E, F, G$ theo thứ tự là trung điểm của các đoạn thẳng $OA, OD$ và $BC$. Chứng minh rằng tam giác $EFG$ là tam giác đều.

Lời giải chi tiết

 

Vì tam giác $ABO$ đều (giả thiết)

$\Rightarrow \widehat {AOB} = \widehat {OAB} = \widehat {ABO} = {60^0}$ (tính chất tam giác đều)

Vì $AB // CD$ (gt)

$\Rightarrow \left\{ \begin{array}{l} \widehat {O{\rm{D}}C} = \widehat {ABO} = {60^0}\left( {so\,le\,trong} \right)\\ \widehat {OC{\rm{D}}} = \widehat {OAB} = {60^0}\left( {so\,le\,trong} \right) \end{array} \right.$

Mà $\widehat {CO{\rm{D}}} = \widehat {AOB} = {60^0}$ (đối đỉnh)

$\Rightarrow$ tam giác $CDO$ cũng đều (dấu hiệu nhận biết tam giác đều)

$\Rightarrow OD = OC$ (tính chất tam giác đều)

Xét $∆AOD$ và $∆BOC$ có:

+) $AO = BO$ (tam giác $ABO$ đều)

+) $\widehat {AO{\rm{D}}} = \widehat {BOC}$ (đối đỉnh)

+) $OD = OC$ (cmt)

$\Rightarrow ∆AOD = ∆BOC$ (c.g.c)

$\Rightarrow AD = BC$ (2 cạnh tương ứng)

Ta có: $E, F$ là trung điểm của $AO$ và $DO$ (gt)

$\Rightarrow$ $EF$ là đường trung bình của tam giác $AOD$ (dấu hiệu nhận biết đường trung bình của tam giác)

 $EF = \dfrac{1}{2}AD = \dfrac{1}{2}BC$   (1) (tính chất đường trung bình của tam giác)

$CF$ là đường trung tuyến của tam giác đều $CDO$ nên $CF ⊥ DO$ (tính chất tam giác đều)

Trong tam giác vuông $CFB$, $FG$ là đường trung tuyến ứng với cạnh huyền nên:

 $FG = \dfrac{1}{2}BC$  (2)

Chứng minh tương tự: 

$BE$ là đường trung tuyến của tam giác đều $ABO$ nên $BE ⊥ AO$ (tính chất tam giác đều)

Trong tam giác vuông $CEB$, $EG$ là đường trung tuyến ứng với cạnh huyền nên:

 $EG = \dfrac{1}{2}BC$  (3) 

Từ (1), (2), (3) suy ra $EF = GF = EG$ nên tam giác $EFG$ là tam giác đều (dấu hiệu nhận biết tam giác đều)

Loigiaihay.com