Bài 104 trang 122 SBT Hình học 10 Nâng cao

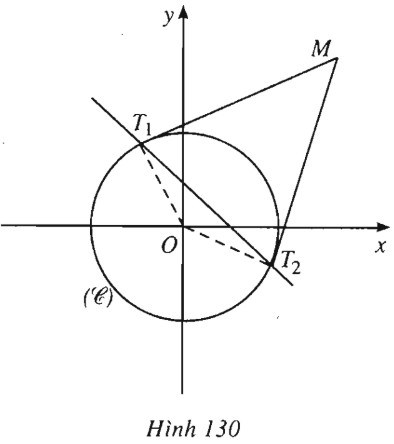
Đề bài

Cho đường tròn \((C): {x^2} + {y^2} = {R^2}\) và điểm \(M(x_0 ; y_0)\) nằm ngoài \((C)\). Từ \(M\) ta kẻ hai tiếp tuyến \(MT_1\) và \(MT_2\) tới \((C)\) (\(T_1, T_2\) là các tiếp điểm).

a) Viết phương trình đường thẳng \(T_1T_2;\)

b) Giả sử \(M\) chạy trên một đường \(d\) cố định không cắt \((C)\). Chứng minh rằng đường thẳng \(T_1T_2\) luôn đi qua một điểm cố định.

Lời giải chi tiết

(h.130).

Giả sử \({T_1} = ({x_1} ; {y_1}) ,  {T_2} = ({x_2} ; {y_2})\). Đường tròn \((C)\) có tâm \(O(0 ; 0)\), bán kính \(R.\) Phương trình tiếp tuyến \(MT_1\) có dạng \({x_1}x + {y_1}y = {R^2}\) và tiếp tuyến \(MT_2\) có dạng

\(\begin{array}{l}{x_2}x + {y_2}y = {R^2}\\M \in M{T_1} , M \in M{T_2}\\    \Rightarrow     \left\{ \begin{array}{l}{x_1}{x_0} + {y_1}{y_0} = {R^2}\\{x_2}{x_0} + {y_2}{y_0} = {R^2}.\end{array} \right.\end{array}\)

Suy ra \(({x_1} ; {y_1}) ,  ({x_2} ; {y_2})\) là các nghiệm của phương trình \({x_0}x + {y_0}y = {R^2}\).    (1)

Vì \(M\) nằm ngoài \((C)\) nên \(x_0^2 + y_0^2 > 0\), do đó (1) là phương trình đường thẳng. 

Vậy phương trình đường thẳng \(T_1T_2\) là \({x_0}x + {y_0}y - {R^2} = 0\).

b) Xét trường hợp đường thẳng cố định \(d\) có phương trình dạng: \(x = a  (|a| > R)\). Khi đó \(M=(a ; y_0)\) phương trình \(T_1T_2\) là \(ax + {y_0}y - {R^2} = 0\). Dễ thấy đường thẳng \(T_1T_2\) luôn đi qua điểm cố định \(\left( { \dfrac{{{R^2}}}{a} ; 0} \right)\).

Xét trường hợp đường thẳng \(d\) có phương trình dạng \(y=kx+m\). Do \(d\) không cắt \((C)\) nên \(m \ne 0\). Ta có \(M = ({x_0} ; k{x_0} + m)\). Phương trình đường thẳng \(T_1T_2\) là

\({x_0}x + (k{x_0} + m)y - {R^2} = 0\) hay \({x_0}(x + ky) + my - {R^2} = 0\).

Ta tìm được điểm cố định mà đường thẳng \(T_1T_2\) luôn đi qua là \(\left( { \dfrac{{ - k{R^2}}}{m} ;  \dfrac{{{R^2}}}{m}} \right)\).

Loigiaihay.com