Bài 10 trang 60 SGK Hình học 10

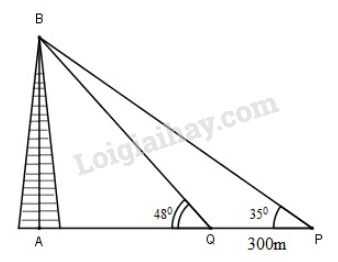
Đề bài

Hai chiếc tàu thủy $P$ và $Q$ cách nhau $300m$.Từ $P$ và $Q$ thẳng hàng với chân $A$ của tháp hải đăng $AB$ ở trên bờ biển người ta nhìn chiều cao $AB$ của tháp dưới các góc $\widehat {BPA} = {35^0},\widehat {BQA} = {48^0}.$ Tính chiều cao của tháp.

Lời giải chi tiết

Tam giác ABQ vuông tại A có: $\cot Q=\frac{AQ}{AB} \Rightarrow AQ = AB\cot48^0$

Tam giác ABP vuông tại A có: $\cot P = \frac{{AP}}{{AB}} \Rightarrow AP = AB\cot {35^0}$ 

$\begin{array}{l} \Rightarrow AP - AQ = AB\cot {35^0} - AB\cot {48^0}\\ \Leftrightarrow PQ = AB\left( {\cot {{35}^0} - \cot {{48}^0}} \right)\\ \Rightarrow AB = \frac{{PQ}}{{\cot {{35}^0} - \cot {{48}^0}}}\\ = \frac{{300}}{{\cot {{35}^0} - \cot {{48}^0}}}\\ = \frac{{300}}{{\frac{1}{{\tan {{35}^0}}} - \frac{1}{{\tan {{48}^0}}}}} \end{array}$

$\approx {{300} \over {1,4281 - 0,9004}}$$\approx 568,457m.$

Loigiaihay.com