Bài 1 trang 19 SGK Hình học 11Cho hình vuông ABCD tâm O (h.1.38) Quảng cáo
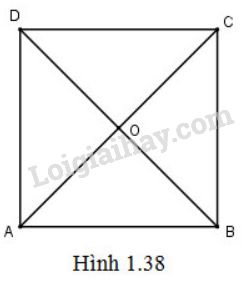
Video hướng dẫn giải Cho hình vuông \(ABCD\) tâm \(O\) (h.1.38)
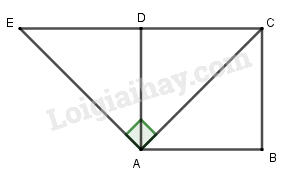
LG a Tìm ảnh của điểm \(C\) qua phép quay tâm \(A\) góc \( 90^{\circ}\) Phương pháp giải: Xác định ảnh: +) Nối \(C\) với \(A\), vẽ tia \(At\) (về phía ngược chiều kim đồng hồ so với tia \(AC\)) sao cho \(\widehat {CAt} = 90^0.\) +) Trên tia \(At\), lấy điểm \(E\) sao cho \(AC = AE.\) Chỉ ra vị trí của điểm \(E.\) Cách khác: Lấy \(E\), chứng tỏ \(E\) là ảnh của \(C\) qua phép quay đó. Lời giải chi tiết: Gọi \(E\) là điểm đối xứng với \(C\) qua tâm \(D\). Ta có: tam giác ACE vuông cân tại A. \( \Rightarrow \left\{ \begin{array}{l} Khi đó \({Q_{(A,90^{\circ})}}^{}\) (C) = \(E\) LG b Tìm ảnh của đường thẳng \(BC\) qua phép quay tâm \(O\) góc \( 90^{\circ}\) Lời giải chi tiết: \(\left\{ \begin{array}{l} \(\left\{ \begin{array}{l} Vậy ảnh của đường thẳng \(BC\) qua phép quay tâm \(O\) góc \( 90^{\circ}\) là đường thẳng \(CD\). Loigiaihay.com
|




















Danh sách bình luận