Trả lời câu hỏi 3 Bài 4 trang 70 SGK Toán 8 Tập 2

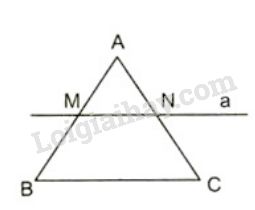
Đề bài

Cho tam giác \(ABC\). Kẻ đường thẳng \(a\) song song với cạnh \(BC\) và cắt hai cạnh \(AB,AC\) theo thứ tự tại \(M\) và \(N\). Hai tam giác \(AMN\) và \(ABC\) có các góc và các cạnh tương ứng như thế nào?

Lời giải chi tiết

Xét tam giác \(ABC\) có \(MN//BC\)

Hai tam giác \(AMN\) và \(ABC\) có:

\(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\) (các cặp góc đồng vị).

\(\widehat {BAC}\) là góc chung.

Mặt khác, theo hệ quả của định lí Ta-lét, hai tam giác \(AMN\) và \(ABC\) có ba cặp cạnh tương ứng tỉ lệ;

\(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} = \dfrac{{MN}}{{BC}}\)

Loigiaihay.com