Lý thuyết về công của lực điện

CÔNG CỦA LỰC ĐIỆN

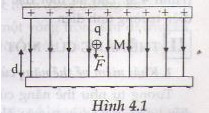
1. Công của lực điện

a) Đặc điểm của lực điện tác dụng lên một điện tích đặt trong một điện trường đều.

- Đặt điện tích q dương (q > 0) tại một điểm M trong điện trường đều (Hình 4.1), nó sẽ chịu tác dụng của một lực điện \(\overrightarrow F  = q.\overrightarrow E \)

- Lực \(\overrightarrow F \) là không đổi, có:

+ phương song song với các đường sức điện

+ chiều hướng từ bản dương sang bản âm

+ độ lớn là F = q.E.

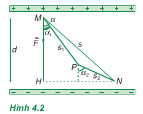
b) Công của lực điện trong điện trường đều.

*  Điện tích Q di chuyển theo đường  thẳng MN, làm với các đường sức điện một góc α, với MN = s (Hình 4.2)

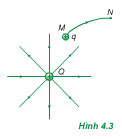
Ta có công của lực điện:

A_MN = \(\overrightarrow F .\overrightarrow s \) = F.s.cosα

Với F = qE và cosα = d thì:

A­_MN = qEd               (4.1)

Trong đó α là góc giữa lực \(\overrightarrow F \) và độ dời \(\overrightarrow s \), d là hình chiếu của độ dời \(\overrightarrow s \) trên một đơn vị đường sức điện.

 + Nếu α < 90⁰ thì cosα >0, do đó d > 0 và A_MN > 0.

 + Nếu α > 90⁰ thif cosα < 0, do đó d < 0 và A_MN < 0.

 Điện tích q di chuyển theo đường gấp khúc MPN. Tương tự như trên, ta có:

A_MPN = Fs₁.cosα₁ + Fs₂cosα₂

Với  s₁.cosα₁ + s₂cosα₂ = d, ta lại có A_MPN  = qEd

Trong đó, d = MH là khoảng cách của hình chiếu từ điểm đầu đến hình chiếu của điểm cuối của đường đi trên một đường sức điện.

* Kết quả có thể mở rộng cho các trường hợp đường đi từ M đến N là một đường gấp khúc hoặc đường cong.

Như vậy, công của lực điện trong sự di chuyển của điện tích trong điện trường đều từ M đến N là

 A_MPN  = qEd, không phụ thuộc vào hình dạng của đường đi mà chỉ phụ thuộc vào vị trí của điểm đầu M và điểm cuối N của đường đi.

c) Công của lực điện trường trong sự di chuyển của điện tích trong điện trường bất kì.

Người ta cũng chứng minh được rằng công của lực điện trong sự di chuyển của điện tích q trong điện trường bất kì từ M đến N không phụ thuộc vào hình dạng đường đi mà chỉ phụ thuộc vào vị trí điểm đầu M và điểm cuối N (Hình 4.3). Đây là một đặc tính chung của trường tĩnh điện.

2. Thế năng cả một điện tích trong điện trường

a) Khái niệm về thế năng của một điện tích trong điện trường

Tương tự như thế năng của một vật trong trọng trường, thế năng của một điện tích q trong điện trường đặc trưng cho khả năng sinh công của lực điện khi đặt điện tích q tại điểm mà ta xét trong điện trường.

Đối với một điện tích q (dương) đặt tại điểm M trong điện trường đều thì công này bằng:

A = qEd = W_M

Trong đó d là khoảng cách từ điểm M đến bản âm; W_M là thế năng của điện tích q tại điểm M.

Trong trường hợp điện tích q nằm tại điểm M trong một điện trường bất kì do nhiều điện tích gây ra thì có thể lấy thế năng bằng công của lực điện khi di chuyển q từ M ra vô cực (A_M∞). Đó là vì ở vô cực, từ là ở rất xa các điện tích gây ra điện trường, thì điện trường bằng không và lực điện coi như hết khả năng sinh công. Do vậy :

W_M = A_M∞

b) Sự phụ thuộc của thế năng W_M vào điện tích q.

Vì độ lớn của lực điện luôn tỉ lệ thuận với điện tích thử q, do đó thế năng của điện tích tại M cũng tỉ lệ thuận với q:

A_{M ­}= W_M­ = V_Mq           (4.3)

V_M­  là một hệ số tỉ lệ, không phụ thuộc q mà chỉ phụ thuộc vào vị trí điểm M trong điện trường.

c) Công của lực điện và độ giảm thế năng.

Khi một điện tích q di chuyển từ một điểm M đến một điểm N trong một điện trường thì công mà lực điện tác dụng lên điện tích đó sinh ra sẽ bằng độ giảm thế năng của điện tích q đặt trong điện trường. 

A_AN = W_M – W­_N             (4.4)

Sơ đồ tư duy về công của lực điện