Lý thuyết tính tương đối của chuyển động. Công thức cộng vận tốcI. Tính tương đối của chuyển động Quảng cáo
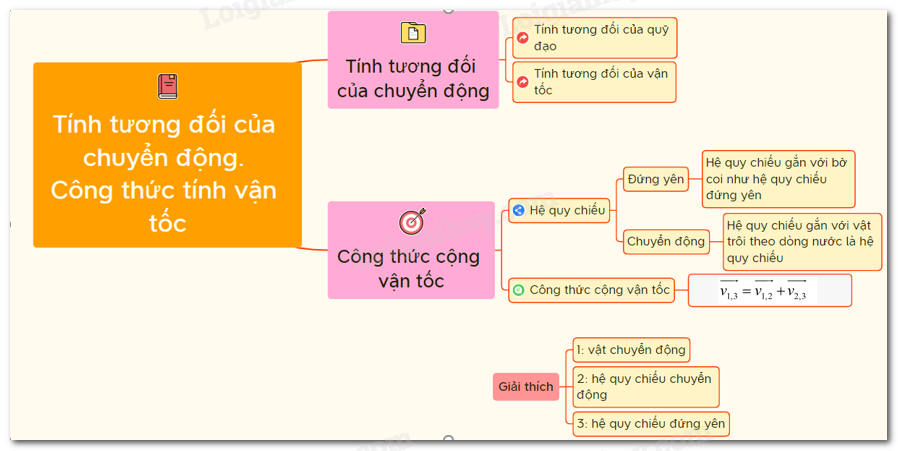
TÍNH TƯƠNG ĐỐI CỦA CHUYỂN ĐỘNG CÔNG THỨC CỘNG VẬN TỐC I. Tính tương đối của chuyển động - Hình dạng quỹ đạo của chuyển động trong các hệ quy chiếu khác nhau thì khác nhau. Quỹ đạo có tính tương đối. - Vận tốc của chuyển động đối với các hệ quy chiếu khác nhau thì khác nhau. Vận tốc có tính tương đối. II. Công thức cộng vận tốc a) Hệ quy chiếu đứng yên và hệ quy chiếu chuyển động - Hệ quy chiếu gắn với vật đứng yên gọi là hệ quy chiếu đứng yên. - Hệ quy chiếu gắn với vật chuyển động gọi là hệ quy chiếu chuyển động. b) Công thức cộng vận tốc Véc tơ vận tốc tuyệt đối \((\overrightarrow {{v_{1,3}}})\) bằng tổng véc tơ vận tốc tương đối \((\overrightarrow {{v_{1,2}}})\) và vận tốc kéo theo \((\overrightarrow {{v_{2,3}}})\). \(\overrightarrow {{v_{1,3}}} = \overrightarrow {{v_{1,2}}} + \overrightarrow {{v_{2,3}}} \) Trong đó số 1 ứng với vật chuyển động, số 2 ứng với hệ quy chiếu chuyển động, số 3 ứng với hệ quy chiếu đứng yên. + Vận tốc tuyệt đối là vận tốc của vật đối với hệ quy chiếu đứng yên + Vận tốc tương đối là vận tốc của vật đối với hệ quy chiếu chuyển động + Vận tốc kéo theo là vận tốc của hệ quy chiếu chuyển động đối với hệ quy chiếu đứng yên. - Trường hợp \(\overrightarrow {{v_{12}}} \) cùng phương, cùng chiều \(\overrightarrow {{v_{23}}} \): + Về độ lớn: \({v_{13}} = {v_{12}} + {v_{23}}\) + Về hướng: \(\overrightarrow {{v_{13}}} \) cùng hướng với \(\overrightarrow {{v_{12}}} \) và \(\overrightarrow {{v_{23}}} \) - Trường hợp \(\overrightarrow {{v_{12}}} \) cùng phương, ngược chiều \(\overrightarrow {{v_{23}}} \) + Về độ lớn: \({v_{13}} = \left| {{v_{12}} - {v_{23}}} \right|\) + Về hướng: \(\overrightarrow {{v_{13}}} \) cùng hướng với \(\overrightarrow {{v_{12}}} \) khi \({v_{12}} > {v_{23}}\) \(\overrightarrow {{v_{13}}} \) cùng hướng với \(\overrightarrow {{v_{23}}} \) khi \({v_{23}} > {v_{12}}\) Sơ đồ tư duy về tính tương đối của chuyển động - Công thức cộng vận tốc
|




















Danh sách bình luận