Luyện tập 1 trang 106 Tài liệu dạy – học Toán 8 tập 1Giải bài tập Cho tứ giác ABCD có AB = BC và CA là tia phân giác của góc BCD. Đường thẳng vuông góc với AC tại A cắt đường thẳng CD ở E. Gọi M là trung điểm của AC. Quảng cáo
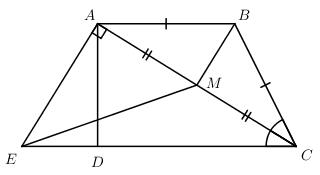
Đề bài Cho tứ giác ABCD có AB = BC và CA là tia phân giác của góc BCD. Đường thẳng vuông góc với AC tại A cắt đường thẳng CD ở E. Gọi M là trung điểm của AC. a) Chứng minh rằng tứ giác ABCD là hình thang. b) Chứng minh rằng tứ giác ABME là hình thang. Lời giải chi tiết
a) Ta có: cân tại B Mà (CA là phân giác của ) Nên Lại có và là hai góc so le trong. Do đó AB // CD Vậy tứ giác ABCD là hình thang. b) ∆ABC cân tại B có BM là đường trung tuyến (M là trung điểm của AC) => BM cũng là đường cao của ∆ABC Mà nên BM // AC Vậy tứ giác ABME là hình thang. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
|
Tải app
