Bài 18. Điện trường đều trang 34, 35, 37, 38 SBT Vật lí 11 Kết nối tri thức với cuộc sống

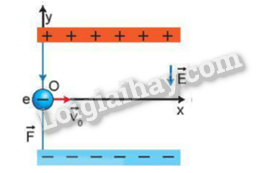
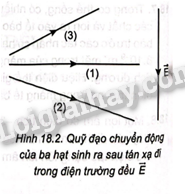
18.1

Cường độ điện trường đều giữa hai bản kim loại phẳng song song được nối với nguồn điện có hiệu điện thế U sẽ giảm đi khi

A, tăng hiệu điện thế giữa hai bản phẳng.

B. tăng khoảng cách giữa hai bản phẳng.

C. tăng diện tích của hai bản phẳng.

D. giảm diện tích của hai bản phẳng.

Phương pháp :

Cường độ điện trường giữa hai bản phẳng này có độ lớn bằng tỉ số giữa hiệu điện thế giữa hai bản phẳng và khoảng cách giữa chúng :\(\)\(E = \frac{U}{d}\)

Lời giải chi tiết :

Ta có : \(E = \frac{U}{d}\)=> E sẽ giảm khi U giảm và d tăng .

Đáp án : B

18.2

Điện trường đều tồn tại ở

A. xung quanh một vật hình cầu tích điện đều.

B. xung quanh một vật hình cầu chỉ tích điện đều trên bề mặt.

C. xung quanh hai bản kim loại phẳng, song song, có kích thước bằng nhau.

D. trong một vùng không gian hẹp gần mặt đất.

Phương pháp :

Điện trường giữa hai bản phẳng nhiễm điện trái dầu đặt song song là điện trường đều

Lời giải chi tiết :

Điện trường đều tồn tại ở xung quanh hai bản kim loại phẳng, song song, có kích thước bằng nhau

Đáp án : C

18.3

Các đường sức điện trong điện trường đều

A. chỉ có phương là không đổi.

B. chỉ có chiều là không đổi.

C. là các đường thẳng song song cách đều.

D. là những đường thẳng đồng quy.

Phương pháp :

Tính chất của điện trường đều.

Lời giải chi tiết :

Các đường sức trong điện trường đều là các đường thẳng song song và cách đều nhau

Đáp án : C

18.4

Khoảng cách giữa hai cực của ống phóng tia X (Hình 18.1) bằng 2 cm, hiệu điện thế giữa hai cực là 100 kV. Cường độ điện trường giữa hai cực bằng:

A. 200 V/m.

B. 50 V/m.

C. 2 000 V/m

D. 5 000 000 V/m

Phương pháp :

Cường độ điện trường giữa hai bản phẳng này có độ lớn bằng tỉ số giữa hiệu điện thế giữa hai bản phẳng và khoảng cách giữa chúng :\(\)\(E = \frac{U}{d}\)

Lời giải chi tiết :

Ta có : \(E = \frac{U}{d} = \frac{{{{100.10}^3}}}{{{{2.10}^{ - 3}}}} = 50000000V/m\)

Đáp án : D

18.5

Trong ống phóng tia X ở Bài 18.4, một electron có điện tích \(e =  - 1,{6.10^{ - 19}}C\) bật ra khỏi bản cực âm (catôt) bay vào điện trường giữa hai bản cực. Lực điện tác dụng lên electron đó bằng

A. 8.\({10^{ - 13}}\) N.

B. 8. \({10^{ - 18}}\) N.

C. 3,2. \({10^{ - 17}}\)N.

 D. 8. \({10^{ - 15}}\)N.

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q}\)

Lời giải chi tiết :

Ta có Lực điện tác dụng lên electron đó : \(\overrightarrow E  = \frac{{\overrightarrow F }}{q} =  > F = E.\left| q \right| = 5000000.1,{6.10^{ - 19}} = {8.10^{ - 13}}N\)

Đáp án: A

18.6

lon âm \(O{H^ - }\)được phát ra từ một máy lọc không khí ở nơi có điện trường

trái đất bằng 120 V/m hướng thẳng đứng từ trên xuống dưới. Hãy xác định lực điện của Trái Đất tác dụng lên ion âm nói trên và vẽ hình minh hoạ.

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q}\)

Lời giải chi tiết :

Đặt gốc tọa độ tại điểm ion âm bắt đầu vào điện trường đều . Trục Ox có hướng trùng với vecto vận tốc ban đầu , trục Oy hướng thẳng đứng lên trên .

Ta thấy vecto cường độ điện trường hướng từ trên xuống dưới và ngược chiều với Oy nên hình chiếu trên phương Oy sẽ có giá trị âm .

Lực điện của Trái Đất tác dụng lên ion âm có giá trị bằng :

\(F =  - E.q = 120.1,{6.10^{ - 19}} = {192.10^{ - 13}}N\)

18.7

Trong cơ thể sống, có nhiều loại tế bào, màng tế bào có nhiệm vụ kiểm soát” các chất và ion ra vào tế bào đảm bảo cho quá trình trao đổi chất và bảo vệ tế bào trước các tác nhân có hại của môi trường. Một tế bào có màng dày khoảng 8. \({10^{ - 9}}\) m, mặt trong của màng tế bào mang điện tích âm, mặt ngoài mang điện tích dương. Hiệu điện thế giữa hai mặt này bằng 0,07 V. Hãy tính cường độ điện trường trong màng tế bào trên.

Phương pháp :

Cường độ điện trường giữa hai bản phẳng này có độ lớn bằng tỉ số giữa hiệu điện thế giữa hai bản phẳng và khoảng cách giữa chúng :\(\)\(E = \frac{U}{d}\)

Lời giải chi tiết :

Cường độ điện trường trong màng tế bào \(E = \frac{U}{d} = \frac{{0,07}}{{{{8.10}^{ - 9}}}} = 8750000V/m\)

18.8

Một ion âm có điện tích \( - 3,{2.10^{ - 19}}\)C đi vào trong màng tế bào ở Bài 18.7.

Hãy xác định xem ion âm sẽ bị đẩy ra khỏi tế bào hay đẩy vào trong tế bào và

lực điện tác dụng lên ion âm bằng bao nhiêu.

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q}\)

Lời giải chi tiết :

Ta có mặt trong của màng tế bào mang điện tích âm, mặt ngoài mang điện tích dương nên điện tích dương bên ngoài sẽ hút ion âm ra khỏi tế bào.

Lực điện tác dụng lên ion âm bằng: \(F = E\left| q \right| = 8750000.3,{2.10^{ - 19}} = 2,{8.10^{ - 12}}N\)

18.9

Cho hai tấm kim loại phẳng rộng, đặt nằm ngang, song song với nhau và

cách nhau d = 5 cm. Hiệu điện thế giữa hai tắm đó bằng 500 V.

a) Tính cường độ điện trường trong khoảng giữa hai bản phẳng.

b) Khi một electron bật ra khỏi bản nhiễm điện âm và đi vào khoảng giữa hai

bản phẳng với tốc độ ban đầu \({v_0} \approx 0\), hãy tính động năng của electron trước

khi va chạm với bản nhiễm điện dương.

Phương pháp :

Cường độ điện trường giữa hai bản phẳng này có độ lớn bằng tỉ số giữa hiệu điện thế giữa hai bản phẳng và khoảng cách giữa chúng :\(\)\(E = \frac{U}{d}\)

Lời giải chi tiết :

a) Cường độ điện trường trong khoảng giữa hai bản phẳng : \(E = \frac{U}{d} = \frac{{500}}{{{{5.10}^{ - 3}}}} = 100000V/m\)

b) Ta có \(\frac{{m{v^2}}}{2} - \frac{{mv_0^2}}{2} = A\)mà \({v_0} \approx 0\) =>

Động năng của electron trước khi va chạm với bản nhiễm điện dương \({W_d} = \frac{{m{v^2}}}{2} = A = eU = {8.10^{ - 17}}(J)\)

18.10

Khi một điện tích chuyển động vào điện trường đều theo phương vuông góc với đường sức điện thì yếu tố nào sẽ luôn giữ không đổi?

A. Gia tốc của chuyển động.

B. Phương của chuyển động.

C. Tốc độ của chuyển động.

D. Độ dịch chuyển sau một đơn vị thời gian.

Phương pháp :

Tác dụng của điện trường đều đối với chuyển động của một điện tích .

Lời giải chi tiết :

Chuyển động này được coi là chuyển động ném ngang . Trong chuyển động ném ngang thì gia tốc tại vị trí bất kì luôn có phương thẳng đứng chiều hướng xuống dưới ó đây là gia tốc trọng trường không đổi

Đáp án : A

18.11

Khi một điện tích chuyển động vào điện trường đều theo phương vuông góc với đường sức điện thì điện trường sẽ không ảnh hưởng tới

A. gia tốc của chuyển động.

B. thành phần vận tốc theo phương vuông góc với đường sức điện.

C. thành phần vận tốc theo phương song song với đường sức điện.

D. quỹ đạo của chuyển động.

Phương pháp :

Tác dụng của điện trường đều đối với chuyển động của một điện tích .

Lời giải chi tiết :

Khi một điện tích bay vào điện trường đều theo phương vuông góc với đường sức, dưới tác dụng của lực điện trường vận tốc theo phương vuông góc với đường sức không thay đổi.

Đáp án : B

18.12

Quỹ đạo chuyển động của một điện tích điểm q bay vào một điện trường đều theo phương vuông góc với đường sức không phụ thuộc vào yếu tố nào sau đây?

A. Độ lớn của điện tích q.

B. Cường độ điện trường E.

C. Vị trí của điện tích q bắt đầu bay vào điện trường.

D. Khối lượng m của điện tích.

Phương pháp :

Tác dụng của điện trường đều đối với chuyển động của một điện tích .

Lời giải chi tiết :

Chuyển động này được coi là chuyển động ném ngang.Quỹ đạo có dạng \(\)\(y = \frac{{a{x^2}}}{{2v_0^2}}\) mà ta có \(a = \frac{F}{m} = \frac{{\left| q \right|E}}{m}\)=> quỹ đạo phụ thuộc vào E , q , m

Đáp án : C

18.13

Máy gia tốc có thể gia tốc cho các hạt mang điện tới tốc độ đủ lớn rồi cho va chạm (hay còn gọi là tán xạ) với hạt khác mà người ta gọi là hạt bia để tạo ra các hạt mới giúp tìm hiểu cấu trúc của vật chất. Trong một quá trình tán xạ như vậy, người ta cho các hạt mới sinh ra đi qua điện trường đều E để kiểm tra điện tích của chúng và xác định hình 18.2.  Hãy cho biết đánh giá nào dưới đây là đúng.

A. Hạt (1) không mang điện, hạt (2) mang điện dương, hạt (3) mang điện âm.

B. Hạt (1) không mang điện, hạt (2) mang điện âm, hạt (3) mang điện dương.

C. Cả 3 hạt cùng không mang điện.

D. Cả 3 đánh giá A, B, C đều có thể xảy ra.

Phương pháp :

Tác dụng của điện trường đều đối với chuyển động của một điện tích .

Lời giải chi tiết :

Chuyển động này được coi là chuyển động ném ngang , quỹ đạo chuyển động  của hạt không mang điện trong điện trường đều có dạng là 1 nhánh của parabol . Dựa vào quỹ đạo như hình ta suy ra cả 3 hạt cùng không mang điện .

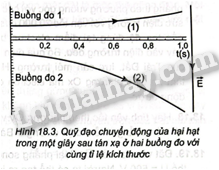
Đáp án : C

18.14

Kết quả tán xạ của hạt electron (\({q_1} =  - 1,{6.10^{ - 19}}\)C) và positron (\({q_2} =  + 1,{6.10^{ - 19}}\)C) trong máy gia tốc ở năng lượng cao cho ra hai hạt. Để xác định điện tích và khối lượng của hai hạt này người ta cho chúng đi vào hai buồng đo có điện trường đều và cường độ điện trường E như nhau theo phương vuông góc với đường sức. Hình ảnh quỹ đạo trong 1 s ngay sau quá trình tán xạ với cùng tỉ lệ kích thước như Hình 18.3: Hai quỹ đạo cho ta biết

A. hạt (1) có điện tích âm, hạt (2) có điện tích dương, độ lớn hai điện tích

khác nhau.

B. hạt (1) có điện tích dương, hạt (2) có điện tích âm, độ lớn hai điện tích

khác nhau.

C. hạt (1) có điện tích âm, hạt (2) có điện tích dương, hai hạt khác nhau về

khối lượng.

D. hạt (1) có điện tích âm, hạt (2) có điện tích dương, độ lớn điện tích của

hạt (2) lớn hơn độ lớn điện tích hạt (1).

Phương pháp :

Tác dụng của điện trường đều đối với chuyển động của một điện tích .

Chuyển động này được coi là chuyển động ném ngang

Lời giải chi tiết :

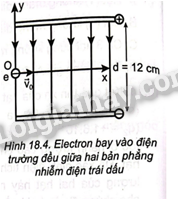
Các đường sức xuất phát từ bản tích điện dương và kết thúc ở bản tích điện âm.Và hai điện tích trái dấu thì hút nhau và hai điện tích cùng dấu thì đẩy nhau.

Dựa vào hình vẽ ta thấy hạt (1) có điện tích âm và hạt (2 ) có điện tích dương và hai hạt có khối lượng khác nhau .

Đáp án :C

18.15

Hãy cho ví dụ về ứng dụng thực tiễn tác dụng của điện trường đối với

chuyển động của điện tích bay vào điện trường đều theo phương vuông góc

với đường sức.

Phương pháp :

Ứng dụng của điện trường đều

Lời giải chi tiết :

Ví dụ về ứng dụng thực tiễn tác dụng của điện trường đối với

chuyển động của điện tích bay vào điện trường đều theo phương vuông góc

với đường sức là : Máy hút ẩm có các ion âm được phát ra theo phương vuông góc với đường sức điện trường của Trái Đất .

Giải thích : Tác dụng của điện trường đều của Trái Đất đối với chuyển động của chùm ion âm: Vì ngay sát bề mặt của Trái Đất có điện trường theo phương thẳng đứng hướng từ trên xuống nên các chùm ion âm luôn bị đẩy và có thể lơ lửng trong không khí. Mà các chất gây ô nhiễm, khói bụi, vi khuẩn,... trong không khí đều mang điện tích dương, vì thế ion âm sẽ hút các ion dương này, trung hòa chúng khiến chúng rơi xuống đất, giúp không khí trở nên sạch sẽ và trong lành hơn

18.16

Một electron bay vào điện trường đều \(\overrightarrow E \) của Trái Đất với vận tốc ban đầu \({v_0}\) theo phương vuông góc với đường sức. Chọn gốc toạ độ là điểm bắt đầu chuyển động của electron trong điện trường đều, trục Oy thẳng đứng hướng lên trên, trục Ox lấy theo chiều \({v_0}\). Viết phương trình quỹ đạo của chuyển động trong điện trường đều.

Phương pháp :

Tác dụng của điện trường đều đối với chuyển động của một điện tích .

Chuyển động này được coi là chuyển động ném ngang

Lời giải chi tiết:

Chọn gốc toạ độ là điểm bắt đầu chuyển động của electron trong điện trường đều, trục Oy thẳng đứng hướng lên trên, trục Ox lấy theo chiều \({v_0}\)

Vecto cường độ điện trường hướng từ trên xuống dưới và ngược chiều với Oy nên hình chiếu trên phương Oy sẽ có giá trị âm .

Lực điện tác dụng lên hạt chiếu lên Oy có giá trị bằng :

\(F =  - qE =  - q\frac{U}{d}\)

- Phương trình chuyển động theo phương Ox : \(x = {v_0}t\) (1)

- Phương trình chuyển động theo phương Oy : \(y = \frac{1}{2}{a_y}{t^2} = \frac{1}{2}\frac{F}{m}{t^2} =  - \frac{1}{2}\frac{{qU}}{{md}}{t^2}\) (2)

Từ (1) và (2) ta thu được phương trình quỹ đạo của chuyển động :

\(y =  - \frac{1}{2}\frac{{qU}}{{md}}{\left( {\frac{x}{{{v_0}}}} \right)^2}\)

18.17

Hai bản phẳng nhiễm điện trái dấu có kích thước lớn và bằng nhau, đặt song song với nhau, cách nhau một khoảng d = 12 cm. Hiệu điện thế giữa hai bản phẳng là 24 V (Hình 18.4). Một electron bay vào chính giữa hai bản phẳng theo phương vuông góc với các đường sức điện trường với vận tốc 20 000 m/s. Chọn gốc toạ độ đúng tại điểm electron bắt đầu bay vào điện trường đều. Bỏ qua điện trường của Trái Đất, lực cản môi trường. Hãy tính tầm xa theo phương Ox mà electron chuyển động được.

Phương pháp :

Tác dụng của điện trường đều đối với chuyển động của một điện tích .

Chuyển động này được coi là chuyển động ném ngang

Lời giải chi tiết:

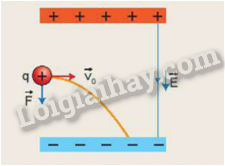
Vật chuyển động theo phương Ox là chuyển động thẳng đều .

Ta có thời gian vật chuyển động hết quỹ đạo :

\(t = \sqrt {\frac{{2h}}{g}}  = \sqrt {\frac{{2.\frac{d}{2}}}{g}}  = \sqrt {\frac{d}{g}}  = \sqrt {\frac{{0,12}}{{10}}} \left( s \right)\)

Tầm xa theo phương Ox mà electron chuyển động được là :

\(L = {v_0}.t = 20000.\sqrt {\frac{{0,12}}{{10}}}  = 2190,89\left( m \right)\)

18.18

Hãy tính vận tốc theo phương Oy và động năng của electron khi va chạm với bản phẳng nhiễm điện dương ở Bài 18.17.

Phương pháp :

Tác dụng của điện trường đều đối với chuyển động của một điện tích .

Chuyển động này được coi là chuyển động ném ngang

Lời giải chi tiết:

Vật chuyển động theo phương Ox là chuyển động rơi tự do .

Ta có thời gian vật chuyển động hết quỹ đạo :

\(t = \sqrt {\frac{{2h}}{g}}  = \sqrt {\frac{{2.\frac{d}{2}}}{g}}  = \sqrt {\frac{d}{g}}  = \sqrt {\frac{{0,12}}{{10}}} \left( s \right)\)

Vận tốc theo phương Oy :\({v_y} = gt = 10.\sqrt {\frac{{0,12}}{{10}}}  = \sqrt {\frac{6}{5}}  \approx 1,095\left( {m/s} \right)\)

Động năng của electron  khi va chạm với bản nhiễm điện dương \({W_d} = A = qU = 1,{6.10^{ - 19}}.24 = 38,{4.10^{ - 19}}(J)\)

18.19

Đặt vào hai bản kim loại phẳng song song, cách nhau 2 cm một hiệu điện thế U = 500 V. Người ta có thể tạo ra ion bằng cách thổi hơi ẩm vào giữa hai bản phẳng này. Giả sử hơi ẩm được thổi vào với vận tốc 50 m/s, một phân tử \({H_2}O\) ở vị trí cách đều hai bản phẳng bị tách thành một ion \(O{H^ - }\) (khối lượng \({m_1} = 2,{833.10^{ - 26}}\) kg, điện tích \({q_1} =  - 1,{6.10^{ - 19}}\)C) và một ion \({H^ + }\)(khối lượng

\({m_2} = 0,{1678.10^{ - 26}}\)kg, điện tích \({q_2} =  + 1,{6.10^{ - 19}}\)C). Bỏ qua các loại lực cản môi

trường, hãy xác định phương trình quỹ đạo cho chuyển động tiếp theo của hai

ion này và vẽ hình minh hoạ.

Phương pháp :

Tác dụng của điện trường đều đối với chuyển động của một điện tích .

Chuyển động này được coi là chuyển động ném ngang

Lời giải chi tiết:

Chọn gốc toạ độ là điểm bắt đầu chuyển động của electron trong điện trường đều, trục Oy thẳng đứng hướng lên trên, trục Ox lấy theo chiều \({v_0}\)

Vecto cường độ điện trường hướng từ trên xuống dưới và ngược chiều với Oy nên hình chiếu trên phương Oy sẽ có giá trị âm .

Lực điện tác dụng lên hạt chiếu lên Oy có giá trị bằng :

\(F =  - qE =  - q\frac{U}{d}\)

- Phương trình chuyển động theo phương Ox : \(x = {v_0}t\) (1)

- Phương trình chuyển động theo phương Oy : \(y = \frac{1}{2}{a_y}{t^2} = \frac{1}{2}\frac{F}{m}{t^2} =  - \frac{1}{2}\frac{{qU}}{{md}}{t^2}\) (2)

Từ (1) và (2) ta thu được phương trình quỹ đạo của chuyển động :

\(y =  - \frac{1}{2}\frac{{qU}}{{md}}{\left( {\frac{x}{{{v_0}}}} \right)^2}(3)\)

Thay số vào (3)  ta được  Phương trình quỹ đạo cho chuyển động tiếp theo của ion \(O{H^ - }\)

\({y_{O{H^ - }}} =  - \frac{1}{2}\frac{{qU}}{{md}}{\left( {\frac{x}{{{v_0}}}} \right)^2} =  - \frac{1}{2}\frac{{( - 1,{{6.10}^{ - 19}}).500}}{{2,{{833.10}^{ - 26}}.0,02}}{\left( {\frac{x}{{50}}} \right)^2} = 2,{824.10^7}.{x^2}(m)\)

Từ pt cho ta thấy ion âm sẽ chuyển động theo cung parabol có bề lõm hướng lên bản phẳng nhiễm điện dương và khi gặp bản này thì chuyển động sẽ kết thúc.

Thay số vào (3)  ta được  Phương trình quỹ đạo cho chuyển động tiếp theo của ion  \({H^ + }\)

\({y_{{H^ + }}} =  - \frac{1}{2}\frac{{qU}}{{md}}{\left( {\frac{x}{{{v_0}}}} \right)^2} =  - \frac{1}{2}\frac{{(1,{{6.10}^{ - 19}}).500}}{{0,{{1678.10}^{ - 26}}.0,02}}{\left( {\frac{x}{{50}}} \right)^2} =  - 4,{768.10^8}.{x^2}(m)\)

Từ pt cho ta thấy ion dương sẽ chuyển động theo cung parabol có bề lõm hướng xuống dưới bản phẳng nhiễm điện âm và khi gặp bản này thì chuyển động sẽ kết thúc.