Bài 17. Khái niệm điện trường trang 31, 32, 33, 34 SBT Vật lí 11 Kết nối tri thức với cuộc sống

17.1

Điện trường được tạo ra bởi điện tích, là dạng vật chất tồn tại quanh điện tích và

A. tác dụng lực lên mọi vật đặt trong nó.

B. tác dụng lực điện lên mọi vật đặt trong nó.

C. truyền lực cho các điện tích.

D. truyền tương tác giữa các điện tích.

Phương pháp :

Khái niệm điện trường

Lời giải chi tiết :

Điện trường được tạo ra bởi điện tích, là dạng vật chất tồn tại quanh điện tích và truyền tương tác giữa các điện tích.

Đáp án : D

17.2

Cường độ điện trường tại một điểm đặc trưng cho điện trường tại điểm đó và

A. phương của vectơ cường độ điện trường.

B. chiều của vectơ cường độ điện trường.

G. phương diện tác dụng lực.

D. độ lớn của lực điện.

Phương pháp :

Tính chất của cường độ điện trường

Lời giải chi tiết :

Cường độ điện trường là đại lượng vật lí đăch trưng cho tác dụng mạnh hay yếu của điện trường tại một điểm

Đáp án : D

17.3

Đơn vị của cường độ điện trường là

A. N

B. N/m.

C. V/m.

D. V.

Phương pháp :

Tính chất của cường độ điện trường

Lời giải chi tiết :

Trong hệ SI , đơn vị của cường độ điện trường là Vôn trên mét (V/m)

Đáp án : C

17.4

Đại lượng nào dưới đây không liên quan tới cường độ điện trường của một điện tích điểm Q đặt tại một điểm trong chân không?

A. Khoảng cách r từ Q đến điểm quan sát.

B. Hằng số điện của chân không.

C. Độ lớn của điện tích Q.

D. Độ lớn của điện tích Q đặt tại điểm quan sát.

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q}\)

Lời giải chi tiết :

Đại lượng không liên quan đến cường độ điện trường của một điện tích điểm Q tại một điểm là điện tích Q đặt tại điểm quan sát vì điện trường tại một điểm được tính bằng công thức:

\(E = k\frac{{\left| Q \right|}}{{\varepsilon {r^2}}}\)

Trong đó ε là hằng số điện môi của môi trường, r là khoảng cách từ vị trí qua sát  đến điện tích Q.

Đáp án : D

17.5

Một điện tích điểm Q < 0 đặt trong chân không. Cường độ điện trường do điện tích Q gây ra tại một điểm M cách Q một khoảng r có phương là đường, thẳng nối Q với M và

A. chiều hướng từ M tới Q với độ lớn bằng \(\frac{Q}{{4\pi {\varepsilon _0}{r^2}}}\)

B. chiều hướng từ M ra xa khỏi Q với độ lớn bằng \(\frac{Q}{{4\pi {\varepsilon _0}{r^2}}}\)

C. chiều hướng từ M tới Q với độ lớn bằng \(\frac{{ - Q}}{{4\pi {\varepsilon _0}{r^2}}}\)

D. chiều hướng từ M ra xa khỏi Q với độ lớn bằng \(\frac{{ - Q}}{{4\pi {\varepsilon _0}{r^2}}}\)

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q}\)

Lời giải chi tiết :

Điện trường tại một điểm được tính bằng công thức:

\(E = k\frac{{\left| Q \right|}}{{\varepsilon {r^2}}} = \frac{Q}{{4\pi {\varepsilon _0}{r^2}}}\)

Trong đó ε là hằng số điện môi của môi trường, r là khoảng cách từ vị trí M đến điện tích Q.

Do Q < 0 => E hướng vào – Q ( Hướng từ M về Q )

Đáp án : A

17.6

Trong chân không đặt có định một điện tích điểm Q = \({2.10^{ - 13}}\)C. Cường độ điện trường tại một điểm M cách Q một khoảng 2 cm có giá trị bằng

A. 2,25 V/m.

B. 4,5 V/m.

C. \(2,{25.10^{ - 4}}\)V/m.

D. \(4,{5.10^{ - 4}}\)V/m

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\)

Lời giải chi tiết :

Cường độ điện trường: \(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}} = \frac{{k\left| Q \right|}}{{{r^2}}} = \frac{{{{9.10}^9}{{.2.10}^{ - 13}}}}{{0,{{02}^2}}} = 4,5(V/m)\)

Đáp án : B

17.7

Trong chân không đặt có định một điện tích điểm Q. Một điểm M cách Q một khoảng r. Tập hợp những điểm có độ lớn cường độ điện trường bằng độ lớn cường độ điện trường tại M là

A. mặt cầu tâm Q và đi qua M.

B. một đường tròn đi qua M.

C. một mặt phẳng đi qua M.

D. các mặt cầu đi qua M.

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\)

Lời giải chi tiết :

Cường độ điện trường tại điểm M là : \(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = k\frac{{\left| Q \right|}}{{{r^2}}}\)

Những điểm có độ lớn cường độ điện trường bằng độ lớn cường độ điện trường tại M là những điểm cách Q một khoảng bằng QM =R

=> Tập hợp những điểm có độ lớn cường độ điện trường bằng độ lớn cường độ điện trường tại M là mặt cầu tâm Q và đi qua M

Đáp án :A

17.8

Khi làm thực nghiệm xác định điện trường tại một điểm M gần mặt đất, người ta dùng điện tích thử q = \({4.10^{ - 16}}\) C xác định được lực điện tác dụng lên điện tích q có giá trị bằng \({5.10^{ - 14}}\) N, có phương thẳng đứng hướng từ trên xuống dưới. Hãy tính độ lớn cường độ điện trường tại điểm M.

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\)

Lời giải chi tiết :

Cường độ điện trường tại điểm M là : \(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{F}{q} = \frac{{{{5.10}^{ - 14}}}}{{{{4.10}^{ - 16}}}} = 125(V/m)\)

17.9

Khi phát hiện một đám mây dông có kích thước nhỏ, một trạm quan sát thời tiết đã đo được khoảng cách từ đám mây đó đền trạm cỡ bằng 6 350 m, người ta cũng xác định được cường độ điện trường do nó gây ra tại trạm cỡ bằng 450 V/m. Hãy ước lượng độ lớn điện tích của đám mây dông đó. Coi đám mây như một điện tích điểm.

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\)

Lời giải chi tiết :

Cường độ điện trường tại đám mây dông là : \(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = k\frac{{\left| Q \right|}}{{{r^2}}} =  > \left| Q \right| = \frac{{E.{r^2}}}{k} = \frac{{{{450.6350}^2}}}{{{{9.10}^9}}} = 2 =  > Q =  \pm 2C\)

17.10

Cường độ điện trường của Trái Đất tại điểm M có giá trị bằng 120 V/m. Một electron có điện tích bằng \(1,{6.10^{ - 19}}\) C và khối lượng bằng \(9,{1.10^{ - 31}}\) kg. Chứng minh rằng, trọng lực có thể được bỏ qua so với lực điện mà Trái Đất tác dụng lên electron. Lấy g = 9,8 \(m/{s^2}\).

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\)

Lời giải chi tiết:

Cường độ điện trường là : \(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{F}{q} =  > F = E.q = 120.1,{6.10^{ - 19}} = 1,{92.10^{ - 17}}N\)

Trọng lực của hạt : \(P = mg = 9,{1.10^{ - 31}}.9,8 = 8,{9.10^{ - 30}}N\)

Ta thấy \(8,{9.10^{ - 30}}N <  <  < 1,{92.10^{ - 17}}N\) => trọng lực có thể được bỏ qua so với lực điện mà Trái Đất tác dụng lên electron => dpcm

17.11

Cường độ điện trường tại một điểm M trong điện trường bất kì là đại lượng

A. vectơ, có phương, chiều và độ lớn phụ thuộc vào vị trí của điểm M.

B. vectơ, chỉ có độ lớn phụ thuộc vào vị trí của điểm M.

C. vô hướng, có giá trị luôn dương.

D. vô hướng, có thể có giá trị âm hoặc dương.

Phương pháp :

Vectơ cường độ điện trường E tại một điểm được xác định bằng tỉ số giữa vectơ lực điện F tác dụng lên một điện tích q đặt tại điểm đó và giá trị của điện tích đó .

Lời giải chi tiết:

Cường độ điện trường tại một điểm M trong điện trường bất kì là đại lượng  vectơ , có chiều phụ thuộc vào dấu của điện tích Q và phương là đường thẳng nối giữa điểm Q và điểm ta đang xét .

Độ lớn của cường độ điện trường bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\) với r là khoảng cách từ M đến Q nên độ lướn của E phụ thuộc vào vị trí của M

Đáp án : B

17.12

Những đường sức điện của điện trường xung quanh một điện tích điểm Q <0 có dạng là

A. những đường cong và đường thẳng có chiều đi vào điện tích Q.

B. những đường thẳng có chiều đi vào điện tích Q.

C. những đường cong và đường thẳng có chiều đi ra khỏi điện tích Q.

D. những đường thẳng có chiều  đi ra khỏi điện tích Q.

Phương pháp :

Tính chất của các đường sức điện.

Lời giải chi tiết :

Các đường sức điện là các đường cong không  kín . Nó xuất phát từ các điện tích dương và tận cùng ở các điện tích âm ( hoặc ở vô cực ) .

Đáp án : A

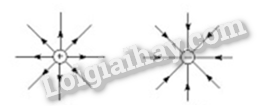
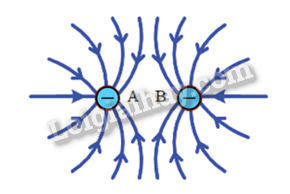
17.13

Đường sức điện cho chúng ta biết về

A. độ lớn của cường độ điện trường của các điểm trên đường sức điện.

B. phương và chiều của cường độ điện trường tại mỗi điểm trên đường sức điện.

C. độ lớn của lực điện tác dụng lên điện tích thử q.

D. độ mạnh yếu của điện trường.

Phương pháp :

Tính chất của các đường sức điện.

Lời giải chi tiết :

Nơi nào có cường độ điện trường lớn hơn thì các đường sức điện ở đó vẽ mau hơn ( dày hơn ) và với nào có cường độ điện trường nhỏ hơn thì các đường sức điện ở đó vẽ thưa hơn.

Đáp án : D

17.14

Hãy vẽ hệ đường sức điện của điện trường xung quanh một điện tích âm đặt trong chân không và nhận xét vị trí có điện trường mạnh.

Phương pháp :

Tính chất của các đường sức điện.

Lời giải chi tiết :

Các đường sức xuất phát từ các điện tích dương và tận cùng ở các điện tích âm ( hoặc ở vô cực )

Ta có hình vẽ hệ đường sức điện của điện trường xung quanh một điện tích âm đặt trong chân không :

Nhận xét : Khoảng cách càng gần về  các điện tích thì đường sức điện càng dày , điện trường càng mạnh

17.15

Hãy vẽ  hệ đường sức điện của điện trường xung quanh hệ hai điện tích âm bằng nhau và xác định những vị trí có điện trường yếu.

Phương pháp :

Tính chất của các đường sức điện.

Lời giải chi tiết :

Các đường sức xuất phát từ các điện tích dương và tận cùng ở các điện tích âm ( hoặc ở vô cực )

Ta có hình vẽ hệ đường sức điện của điện trường xung quanh hệ hai điện tích âm bằng nhau :

Nhận xét : Khoảng cách càng xa các điện tích thì đường sức điện càng thưa dần , điện trường yếu dần.

17.16

Vào một ngày đẹp trời đo đạc thực nghiệm cho thầy gần bề mặt Trái Đất ở một khu vực tại Hà Nội tồn tại điện trường theo phương thẳng đứng, hướng từ trên xuống dưới, có độ lớn cường độ điện trường không đổi trong khu vực khảo sát và bằng 114 V/m.

a) Hãy vẽ hệ đường sức điện của điện trường trái đất ở khu vực đó.

b) Một hạt bụi mịn có điện tích \(6,{4.10^{ - 19}}\) C sẽ chịu tác dụng của lực điện có

phương, chiều và độ lớn như thế nào?         

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\)

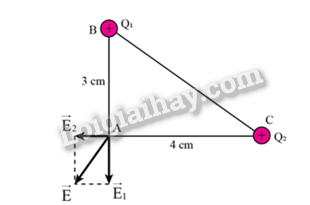
Lời giải chi tiết:

a) Hệ đường sức điện của điện trường trái đất ở khu vực tồn tại điện trường theo phương thẳng đứng, hướng từ trên xuống dưới :

b) Một hạt bụi mịn có điện tích \(6,{4.10^{ - 19}}\) C sẽ chịu tác dụng của lực điện có phương thẳng đứng chiều từ trên xuống dưới ( do ngay sát bề mặt Trái đất tồn tại điện trường theo phương thẳng đứng, hướng từ trên xuống dưới)

Độ lớn lực điện của Trái đất tác dụng lên hạt bụi này là :

\(F = q.E = 6,{4.10^{ - 19}}.114 = 729,{6.10^{ - 19}}N\)

17.17

Đặt điện tích \({Q_1} =  + 6,{4.10^{ - 19}}\) C tại điểm A và điện tích \({Q_2} =  - {2.10^{ - 8}}\)C tại điểm B cách A một khoảng bằng 3 cm. Hãy xác định những điểm mà cường độ điện trường tại đó bằng 0.

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\)

Lời giải chi tiết:

Do điện tích \({Q_1}\)và \({Q_2}\)là trái dấu nên để cường độ điện trường tại M bằng 0 thì M phải nằm ngoài đoạn nối AB

Vì \({Q_2}\) có điện tích nhỏ hơn \({Q_1}\) nên M nằm gần B hơn

Cường độ điện trường tại M bằng 0 nên :

\({E_1} = {E_2} = k\frac{{\left| {{Q_1}} \right|}}{{A{M^2}}} = k\frac{{\left| {{Q_2}} \right|}}{{M{B^2}}} = \frac{{\left| { - {{2.10}^{ - 8}}} \right|}}{{M{B^2}}} = \frac{{\left| {{{6.10}^{ - 8}}} \right|}}{{{{\left( {AB + MB} \right)}^2}}} \Leftrightarrow \)\(\left[ {_{MB \approx  - 0,01(loai)}^{MB \approx 0,04m}} \right.\)

Vậy điểm M cần tìm nằm ngoài AB và cách B một khoảng 4 cm cách A một đoạn 7 cm .

17.18

Cho tam giác ABC vuông tại A có AB = 3 cm và AC =4 cm. Tại B ta đặt điện tích \({Q_1} = 4,{5.10^{ - 8}}\), tại C, ta đặt điện tích \({Q_2} = {2.10^{ - 8}}\)C. Hãy tính độ lớn của cường độ điện trường do hai điện tích này gây ra tại A.

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\)

Lời giải chi tiết:

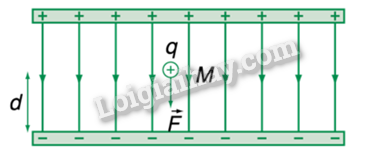
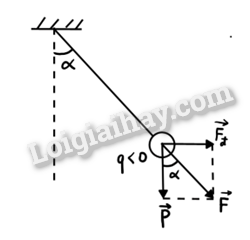
Cường độ điện trường do điện do điện tích \({Q_1} = 4,{5.10^{ - 8}}C\) gây ra tại A là

\({E_1} = k\frac{{\left| {{Q_1}} \right|}}{{A{B^2}}} = {9.10^9}\frac{{4,{{5.10}^{ - 8}}}}{{0,{{03}^2}}} = 4,{5.10^5}V/m\)

Cường độ điện trường do điện do điện tích \({Q_2} = {2.10^{ - 8}}C\)  gây ra tại A là

\({E_2} = k\frac{{\left| {{Q_2}} \right|}}{{A{C^2}}} = {9.10^9}\frac{{{{2.10}^{ - 8}}}}{{0,{{04}^2}}} = 1,{125.10^5}V/m\)

17.19

Hai điểm A và B cách nhau 6 om. Tại A, đặt điện tích \({Q_1} =  + {8.10^{ - 10}}\)C. Tại B, đặt điện tích \({Q_2} =  + {2.10^{ - 10}}\)C. Hãy xác định những điểm mà cường độ điện trường tại đó bằng 0.

Phương pháp :

Độ lớn của cường độ điện trường do một điện tích điểm Q đặt trong chân không hoặc trong không khí gây ra tại một điểm cách nó một khoảng r có giá trị bằng: \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\)

Lời giải chi tiết:

Do điện tích \({Q_1}\)và \({Q_2}\)là cùng dấu nên để cường độ điện trường tại M bằng 0 thì M phải nằm trong đoạn nối AB .

Vì \({Q_2}\) có điện tích nhỏ hơn \({Q_1}\) nên M nằm gần B hơn

Cường độ điện trường tại M bằng 0 nên :

\({E_1} = {E_2} = k\frac{{\left| {{Q_1}} \right|}}{{A{M^2}}} = k\frac{{\left| {{Q_2}} \right|}}{{M{B^2}}} = \frac{{\left| {{{6.10}^{ - 8}}} \right|}}{{A{M^2}}} = \frac{{\left| { - {{2.10}^{ - 8}}} \right|}}{{{{\left( {AB - AM} \right)}^2}}} = \frac{{\left| {{{6.10}^{ - 8}}} \right|}}{{A{M^2}}} = \frac{{\left| {{{2.10}^{ - 8}}} \right|}}{{{{\left( {0,06 - AM} \right)}^2}}} \Leftrightarrow \)\(\left[ {_{AM \approx 0,15(loai)}^{AM \approx 0,038m}} \right.\)

Vậy điểm M cần tìm nằm trong AB và cách A một khoảng 3,8  cm cách B một đoạn 2,2 cm 

17.20

Trong thí nghiệm về điện trường (Hình 17.1), người ta tạo ra một điện trường giống nhau tại mọi điểm giữa hai bản kim loại hình tròn với E = \({10^5}\)V/m, có phương nằm ngang và hướng từ tấm bên phải (+) sang tấm bên trái (-). Một viên bi nhỏ khối lượng 0,1 g, tích điện âm q = \({10^{ - 8}}\) C được móc bằng hai dây chỉ và treo vào giá như hình. Hãy tính góc lệch của mặt phẳng tạo bởi hai dây mặt phẳng thẳng đứng. Lấy g = 10 \(m/{s^2}\)

Phương pháp :

Độ lớn của cường độ điện trường : \(\)\(\overrightarrow E  = \frac{{\overrightarrow F }}{q} = \frac{{\left| Q \right|}}{{4\pi {\varepsilon _0}{r^2}}}\)

Lời giải chi tiết:

Khi vật thẳng đứng => Vật cân bằng \( =  > {F_d} = P.\tan \alpha  =  > \left| q \right|E = mg\tan \alpha \)

 \( =  > \tan \alpha  = \frac{{\left| q \right|E}}{{mg}} = \frac{{{{10}^{ - 8}}{{.10}^5}}}{{0,{{1.10}^{ - 3}}.10}} = 1 =  > \alpha  = \frac{\pi }{4}(rad)\)