Phần câu hỏi bài 9 trang 101 Vở bài tập toán 8 tập 2Giải phần câu hỏi bài 9 trang 101 VBT toán 8 tập 2. Cho hình vẽ 48. Hãy viết các cặp tam giác đồng dạng (theo đúng thứ tự các đỉnh tương ứng) vào chỗ trống:... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
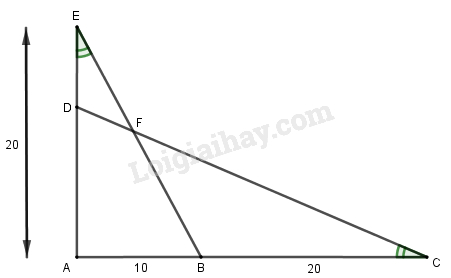
Câu 19a a) Cho hình vẽ 48. Hãy viết các cặp tam giác đồng dạng (theo đúng thứ tự các đỉnh tương ứng) vào chỗ trống:
\(\begin{array}{l}{a_1})\,\Delta ....... \backsim \Delta .......\\{a_2})\,\Delta ....... \backsim \Delta .......\end{array}\) Phương pháp giải: Sử dụng trường hợp đồng dạng thứ ba: Hai tam giác có hai cặp góc tương ứng bằng nhau thì đồng dạng với nhau. Giải chi tiết: Xét tam giác \(ABE\) và tam giác \(ADC\) có: Chung \(\widehat A\) \(\widehat {AEB} = \widehat {ACD}\left( {gt} \right)\) \( \Rightarrow \Delta ABE \backsim \Delta ADC\left( {g.g} \right)\) Xét tam giác \(DEF\) và tam giác \(BCF\) có: \(\widehat {DEF} = \widehat {BCF}\left( {gt} \right)\) \(\widehat {DFE} = \widehat {BFC}\) (hai góc đối đỉnh) Suy ra \(\Delta DEF \backsim \Delta BCF\left( {g.g} \right)\) Vậy ta điền như sau: \(\begin{array}{l}{a_1})\,\Delta ABE \backsim \Delta ADC\\{a_2})\,\Delta DEF \backsim \Delta BCF\end{array}\) Câu 19b b) Cho biết \(AB = 10,BC = 20,AE = 20\). \({b_1})\) Độ dài của đoạn thẳng \(DE\) là: A. \(5\) B. \(6,5\) C. \(5,5\) D. \(7\) Khoanh tròn vào chữ cái trước khẳng định đúng. Phương pháp giải: Sử dụng kết quả câu a, từ hai tam giác đồng dạng suy ra các tỉ số đồng dạng và tính toán. Giải chi tiết: Theo câu a) \(\Delta ABE \backsim \Delta ADC\)\( \Rightarrow \dfrac{{AB}}{{AD}} = \dfrac{{AE}}{{AC}}\) \( \Rightarrow \dfrac{{10}}{{AD}} = \dfrac{{20}}{{10 + 20}}\) \( \Rightarrow AD = \dfrac{{10.30}}{{20}} = 15\) Suy ra \(DE = AE - AD\) \( = 20 - 15 = 5\). Chọn A. \({b_2})\) (Tính chính xác đến hai chữ số thập phân). Độ dài của đoạn thẳng \(CD\) là: A. \(30,25\) B. \(35,45\) C. \(33,54\) D. \(32,25\) Khoanh tròn vào chữ cái trước khẳng định đúng. Phương pháp: Sử dụng định lí Pi – ta – go trong tam giác vuông. Cách giải: Tam giác \(ACD\) vuông tại \(A\) nên \(A{C^2} + A{D^2} = C{D^2}\) \( \Rightarrow {\left( {10 + 20} \right)^2} + {15^2} = C{D^2}\) \( \Rightarrow C{D^2} = 1125 \Rightarrow CD \approx 33,54\). Chọn C. \({b_3})\) Cho biết độ dài của đoạn \(CF = 29,8\). Độ dài của đoạn thẳng \(EF\) là: A. \(7,45\) B. \(7,55\) C. \(7,65\) D. \(7,75\) Khoanh tròn vào chữ cái trước khẳng định đúng. Phương pháp: Sử dụng kết quả câu a), từ hai tam giác đồng dạng suy ra các tỉ số và tính toán. Cách giải: Từ câu a) ta có \(\Delta DEF \backsim \Delta BCF\)\( \Rightarrow \dfrac{{DE}}{{BC}} = \dfrac{{EF}}{{CF}} \Rightarrow \dfrac{5}{{20}} = \dfrac{{EF}}{{29,8}}\) \( \Rightarrow EF = \dfrac{{5.29,8}}{{20}} = 7,45\) Chọn A. Loigiaihay.com
|




















Danh sách bình luận