Phần câu hỏi bài 8 trang 33 Vở bài tập toán 6 tập 2Giải phần câu hỏi bài 8 trang 33 VBT toán 6 tập 2. Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được khẳng định đúng... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Câu 22 Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được khẳng định đúng :
Phương pháp giải: Đổi chỗ các phân số cùng mẫu rồi thực hiện phép cộng. Lời giải chi tiết: \(\begin{array}{l}\dfrac{{ - 2}}{3} + \dfrac{3}{4} + \dfrac{{ - 4}}{5} + \dfrac{5}{6} + \dfrac{4}{5} + \dfrac{3}{{ - 4}} + \dfrac{2}{3}\\ = \left( {\dfrac{{ - 2}}{3} + \dfrac{2}{3}} \right) + \left( {\dfrac{3}{4} + \dfrac{3}{{ - 4}}} \right) + \left( {\dfrac{{ - 4}}{5} + \dfrac{4}{5}} \right) + \dfrac{5}{6}\\ = \dfrac{5}{6}\end{array}\) (A) nối với ý 5) \(\begin{array}{l}\dfrac{{ - 1}}{7} + \dfrac{1}{8} + \dfrac{7}{{18}} + \dfrac{7}{8} + \dfrac{{ - 6}}{7}\\ = \left( {\dfrac{{ - 1}}{7} + \dfrac{{ - 6}}{7}} \right) + \left( {\dfrac{1}{8} + \dfrac{7}{8}} \right) + \dfrac{7}{{18}}\\ = - 1 + 1 + \dfrac{7}{{18}}\\ = \dfrac{7}{{18}}\end{array}\) (B) nối với ý 4) \(\begin{array}{l}\dfrac{7}{{11}} + \dfrac{9}{{11}} + \dfrac{{13}}{{11}} + \dfrac{{15}}{{11}} + \dfrac{{ - 36}}{{18}}\\ = \dfrac{{44}}{{11}} + \left( { - 2} \right)\\ = 4 + \left( { - 2} \right) = 2\end{array}\) (C) nối với ý 3) \(\begin{array}{l}\dfrac{5}{{19}} + \dfrac{{ - 7}}{{14}} + \dfrac{4}{{19}} + \dfrac{{10}}{{19}}\\ = \left( {\dfrac{5}{{19}} + \dfrac{4}{{19}} + \dfrac{{10}}{{19}}} \right) + \dfrac{{ - 7}}{{14}}\\ = 1 + \left( { - \dfrac{1}{2}} \right)\\ = \dfrac{1}{2}\end{array}\) (D) nối với 1). Câu 23 Viết \(\dfrac{2}{3}\) thành tổng của ba phân số tối giản, có mẫu chung là \(15\), tử là số tự nhiên khác \(0\), được kết quả là : (A) \(\dfrac{1}{3} + \dfrac{2}{5} + \dfrac{1}{{15}}\) (B) \(\dfrac{1}{3} + \dfrac{1}{5} + \dfrac{2}{{15}};\) (C) \(\dfrac{1}{3} + \dfrac{3}{5} + \dfrac{1}{{15}};\) (D) \(\dfrac{1}{3} + \dfrac{1}{5} + \dfrac{4}{{15}}.\) Phương pháp giải: Tính tổng bốn đáp án đã cho rồi chọn đáp án đúng nhất. Lời giải chi tiết: \(\begin{array}{l} Chọn B. Câu 24 Điền số nguyên thích hợp vào chỗ trống : (A) \(\dfrac{{ - 37}}{8} + \dfrac{{13}}{8} < ...... < \dfrac{1}{4} + \dfrac{{ - 5}}{4}\) (B) \(\dfrac{{ - 1}}{3} + \dfrac{4}{3} + \dfrac{1}{3} < ...... < \dfrac{3}{4} + \dfrac{3}{2}\) (C) \(\dfrac{4}{{13}} + \dfrac{3}{7} + \dfrac{9}{{13}} + \dfrac{{ - 8}}{{14}} < ...... < \dfrac{{11}}{{33}}\\ + \dfrac{{27}}{9} + \dfrac{{ - 12}}{{53}} + \dfrac{7}{{ - 9}}\) Phương pháp giải: - Tính giá trị của hai vế. - Tìm số nguyên thỏa mãn đề bài rồi điền vào chỗ trống. Lời giải chi tiết: \(\begin{array}{l} Vì \(-3<-2<-1\) nên cần điền vào chỗ trống số \(-2\). \(\begin{array}{l} Vì \(\dfrac{4}{3} < 2 < \dfrac{9}{4}\) nên số cần điền vào chỗ trống là \(2\). \(\begin{array}{l} Ta có :\(\dfrac{6}{7} < 1 < \dfrac{{1111}}{{477}}\) và \(\dfrac{6}{7} < 2 < \dfrac{{1111}}{{477}}\) nên có hai số thỏa mãn để điền vào chỗ trống là \(1\) hoặc \(2\). Loigiaihay.co
|














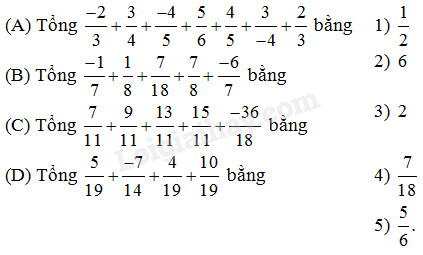






Danh sách bình luận