Phần câu hỏi bài 5 trang 101 Vở bài tập toán 9 tập 2

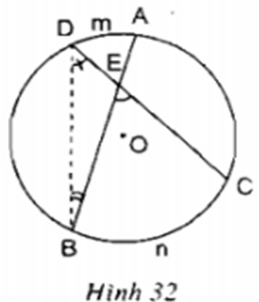
Câu 12.

Hãy ghi công thức tính số đo của góc có đỉnh ở bên tròn đường tròn

\(\widehat {BEC} = \frac{1}{2}\left( {..... - .....} \right)\)

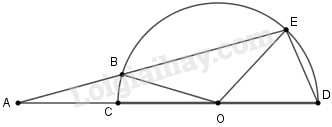
Phương pháp giải:

Sử dụng: Số đo của góc đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

Lời giải chi tiết:

Xét \(\left( O \right)\) ta có \(\widehat {BEC} = \dfrac{1}{2}\)(sđ \(\overparen{BnC}\) + sđ\(\overparen{AmD}\) ) (góc có đỉnh bên trong đường tròn)

Câu 13.

Cho nửa đường tròn tâm (O), đường kính CD. Đặt cung DE có số đo bằng 45^o. Từ E kẻ đường thẳng cắt đường tròn tại B và cắt tia DC kéo dài tại A. Khi AB = OD, số đo của góc BAO là:

(A) 10^o                                     (B) 15^o

(C) 20^o                                     (D) 25^o

Khoanh tròn vào chữ cái trước kết quả đúng. 

Phương pháp giải:

Sử dụng: Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn

Sử dụng tính chất tam giác cân để tính  

Lời giải chi tiết:

Ta có \(AB = OD \Rightarrow AB = OB\) (vì \(OB=OD\) và cùng bằng bán kính đường tròn \(\left( O \right)\)) nên tam giác \(OBA\) cân tại \(B\) \( \Rightarrow \widehat {OAB} = \widehat {BOA}\) (1) (tính chất)

Lại có \(\widehat {BOC} = \) sđ \(\overparen{BC}\) và \(\widehat {BAO} = \dfrac{1}{2}\)(sđ\(\overparen{ED}\) -  sđ\(\overparen{BC}\)) (2)

Từ (1) và (2) suy ra sđ\(\overparen{BC}\) \( = \dfrac{1}{2}\)(sđ\(\overparen{ED} - sđ\overparen{BC}\)) \( \Leftrightarrow \)sđ\(\overparen{BC}\)\( = \dfrac{1}{3}\) sđ \(\overparen{ED}\)

\( = \dfrac{{45^\circ }}{3} = 15^\circ \)

Suy ra \(\widehat {OAB} = \widehat {BOA} = 15^\circ \)

Loigiaihay.com