Phần câu hỏi bài 1 trang 110, 111 Vở bài tập toán 9 tập 1

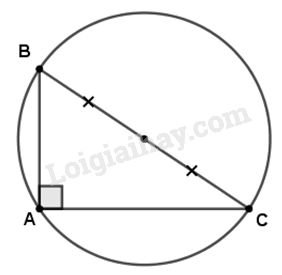
Câu 1.

Cho tam giác ABC vuông tại A. Hãy khoanh tròn vào chữ cái đứng trước khẳng định đúng:

(A) Tâm của đường tròn ngoại tiếp tam giác ABC là một trong ba đỉnh của tam giác đó

(B) Tâm của đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền.

(C) Tâm của đường tròn ngoại tiếp tam giác ABC là trung điểm của một trong hai cạnh góc vuông

(D) Tâm của đường tròn ngoại tiếp tam giác ABC nằm bên trong tam giác đó.

Phương pháp giải:

Xác định điểm cách đều ba đỉnh của tam giác vuông rồi chọn nhận xét đúng.

Lời giải chi tiết:

Tam giác ABC vuông tại A, đường tròn ngoại tiếp tam giác đó có dạng như sau:

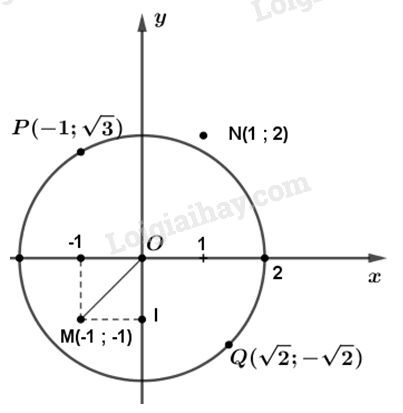
Nhận xét đúng là : Tâm của đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền.

Đáp án cần chọn là B.

Câu 2.

Hãy điền tiếp vào chỗ trống trong các khẳng định dưới đây để được các khẳng định đúng.

Trên mặt phẳng tọa độ Oxy, xét đường tròn tâm O, bán kính 2. Ta có:

(A) Điểm M(-1 ; -1) nằm…….đường tròn (O ; 2)

(B) Điểm N(1 ; 2) nằm…….đường tròn (O ; 2)

(C) Điểm \(P\left( { - 1;\sqrt 3 } \right)\) nằm…….đường tròn (O ; 2)

(D) Điểm \(\left( {\sqrt 2 ; - \sqrt 2 } \right)\) nằm…….đường tròn (O ; 2).

Phương pháp giải:

Để xác định vị trí của điểm \(M\)với đường tròn \(\left( {O;R} \right)\) thì em so sánh khoảng cách \(OM\) với \(R.\)

- Nếu \(OM = R\) thì điểm \(M\) nằm trên đường tròn.

- Nếu \(OM < R\) thì điểm \(M\) nằm trong đường tròn.

- Nếu \(OM > R\) thì điểm \(M\) nằm ngoài đường tròn.

Lời giải chi tiết:

Áp dụng định lí Pi-ta-go, tam giác vuông \(OMI\) có : \(OM = \sqrt {O{I^2} + M{I^2}}  = \sqrt {{1^2} + {1^2}}  = \sqrt 2  < 2.\) 

Vậy điểm \(M\) nằm trong đường tròn \(\left( {O;2} \right)\).

Tương tự ta có : \(ON = \sqrt {{1^2} + {2^2}}\)\(  = \sqrt 5  > 2\)

Điểm N nằm ngoài đường tròn \(\left( {O;2} \right).\)

\(OP = \sqrt {{1^2} + {{\left( {\sqrt 3 } \right)}^2}} \)\( = \sqrt 4  = 2\)

Điểm P nằm trên đường tròn \(\left( {O;2} \right).\)

\(OQ = \sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}}  \)\(= \sqrt 4  = 2\)

Điểm Q nằm trên đường tròn \(\left( {O;2} \right).\)

Vậy điền vào chỗ trống theo thứ tự :

(A) trong

(B) ngoài

(C) trên

(D) trên.

Loigiaihay.com