Giải mục 5 trang 37 SGK Toán 11 tập 1 - Kết nối tri thức

HĐ5

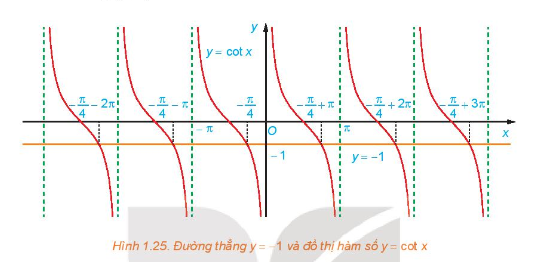
Trả lời câu hỏi Hoạt động 5 trang 37 SGK Toán 11 Kết nối tri thức

a) Quan sát Hình 1.25, hãy cho biết đường thẳng \(y =  - 1\) cắt đồ thị hàm số \(y = \cot x\) tại mấy điểm trên khoảng \(\left( {0;\pi } \right)\)?

b) Dựa vào tính tuần hoàn của hàm cotang, hãy viết công thức nghiệm của phương trình đã cho.

Phương pháp giải:

Nghiệm của phương trình \(\cot x =  - 1\) là hoành độ các giao điểm của đường thẳng \(y =  - 1\) và đồ thị hàm số \(y = \cot x\).

Lời giải chi tiết:

a) Từ Hình 1.25, ta thấy đường thẳng \(y =  - 1\) cắt đồ thị hàm số \(y = \cot x\)tại 1 điểm \(x =  - \frac{\pi }{4} + \pi \) trên khoảng \(\left( {0;\pi } \right)\).

b) Ta có công thức nghiệm của phương trình là: \(x =  - \frac{\pi }{4} + \pi  + k\pi \left( {k \in \mathbb{Z}} \right)\).

LT5

Trả lời câu hỏi Luyện tập 5 trang 37 SGK Toán 11 Kết nối tri thức

Giải các phương trình sau:

a) \(\cot x = 1\);

b) \(\sqrt 3 \cot x + 1 = 0\).

Phương pháp giải:

Sử dụng công thức nghiệm  \(\cot x = m \Leftrightarrow \cot x = \cot \alpha  \Leftrightarrow x = \alpha  + k\pi \left( {k \in \mathbb{Z}} \right)\).

Lời giải chi tiết:

a) \(\cot x = 1 \Leftrightarrow \cot x = \cot \frac{\pi }{4} \Leftrightarrow x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\)

b) \(\sqrt 3 \cot x + 1 = 0 \Leftrightarrow \sqrt 3 \cot x =  - 1 \Leftrightarrow \cot x =  - \frac{{\sqrt 3 }}{3}\)

\(\Leftrightarrow \cot x = \cot \left( { - \frac{\pi }{3}} \right) \Leftrightarrow x =  - \frac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)\)