Giải mục 2 trang 15, 16, 17 Chuyên đề học tập Toán 11 - Chân trời sáng tạo

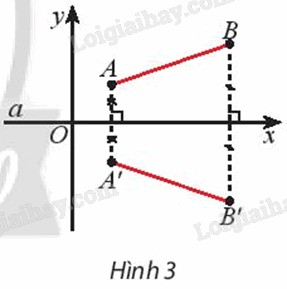
Khám phá 2

Giả sử Đ_a là phép đối xứng trục qua đường thẳng a. Ta chọn hệ tọa độ Oxy sao cho trục Ox trùng với a. Lấy hai điểm tùy ý A(x_A; y_A) và B(x_B; y_B). Gọi A’, B’ lần lượt là ảnh của A, B qua phép đối xứng trục a (Hình 3). Xác định tọa độ của A’ và B’ rồi dùng công thức tính khoảng cách để so sánh A’B’ và AB.

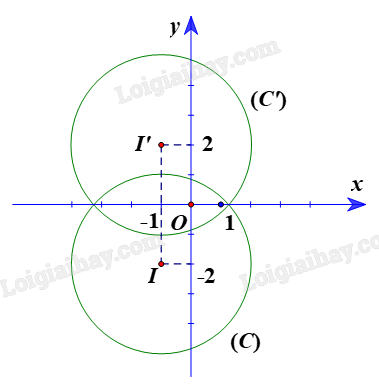
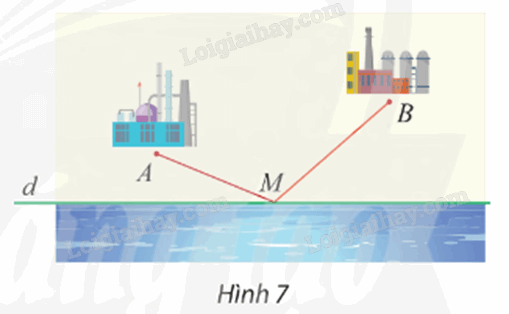
Phương pháp giải:

Công thức tính khoảng cách AB: \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \)

Lời giải chi tiết:

+ Ta có A’ là ảnh của A qua

Suy ra a là đường trung trực của đoạn thẳng AA’ hay Ox là đường trung trực của đoạn thẳng AA’.

Do đó A’ đối xứng với A qua Ox nên chúng có cùng hoành độ và có tung độ đối nhau.

Vì vậy tọa độ \(A'({x_A};{\rm{ }}-{y_A}).\)

Tương tự như vậy, ta được tọa độ \(B'({x_B};{\rm{ }}-{y_B}).\)

Vậy tọa độ \(A'({x_A};{\rm{ }}-{y_A}),{\rm{ }}B'({x_B};{\rm{ }}-{y_B}).\)

+ Ta có \(\overrightarrow {AB}  = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)\).

Suy ra \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \).

Ta lại có \(\overrightarrow {A'B'}  = \left( {{x_B} - {x_A}; - {y_B} + {y_A}} \right)\).

Suy ra:

\(A'B' = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( { - {y_B} + {y_A}} \right)}^2}}  = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} \).

Vậy \(A'B'{\rm{ }} = {\rm{ }}AB.\)

Thực hành 1

Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(d:{\rm{ }}x-y + 3 = 0\) và đường tròn \(\left( C \right):{\rm{ }}{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2}\; = 9.\)

a) Tìm ảnh của đường thẳng d qua \({Đ_{Oy}}.\)

b) Tìm ảnh của đường tròn (C) qua \({Đ_{Ox}}.\)

Phương pháp giải:

Nếu \(M' = {Đ_{Ox}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} =  - {y_M}\end{array} \right.\)

Nếu \(M' = {Đ_{Oy}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} =  - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)

Lời giải chi tiết:

a) Trục \(Oy:{\rm{ }}x = 0.\)

Thế x = 0 vào phương trình d, ta được \(0{\rm{ }}-{\rm{ }}y{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}0 \Leftrightarrow y{\rm{ }} = {\rm{ }}3.\)

Suy ra giao điểm của d và Oy là \(P\left( {0;{\rm{ }}3} \right).\)

Chọn điểm \(M\left( {1;{\rm{ }}4} \right) \in d:{\rm{ }}x{\rm{ }}-{\rm{ }}y{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}0\)

Ta đặt \(M'{\rm{ }} = {\rm{ }}{Đ_{Oy}}\left( M \right).\)

Suy ra Oy là đường trung trực của MM’ hay M’ là điểm đối xứng với M qua Oy.

Do đó hai điểm M và M’ có cùng tung độ và có hoành độ đối nhau.

Vì vậy tọa độ điểm M’(–1; 4).

Ta có \(\overrightarrow {M'P}  = \left( {1; - 1} \right)\)

Gọi d’ là ảnh của d qua \({Đ_{Oy}}.\)

Đường thẳng d’ có vectơ chỉ phương \(\overrightarrow {M'P}  = \left( {1; - 1} \right)\).

Suy ra d’ có vectơ pháp tuyến \({\vec n_{d'}} = \left( {1;1} \right)\)

Vậy đường thẳng d’ đi qua P(0; 3) và có vectơ pháp tuyến \({\vec n_{d'}} = \left( {1;1} \right)\) nên phương trình d’ là: \(1.\left( {x{\rm{ }}-{\rm{ }}0} \right){\rm{ }} + {\rm{ }}1.\left( {y{\rm{ }}-{\rm{ }}3} \right){\rm{ }} = {\rm{ }}0\; \Leftrightarrow x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}3{\rm{ }} = {\rm{ }}0.\)

b) Đường tròn (C) có tâm I(–1; –2), bán kính R = 3.

Ta đặt \(I'{\rm{ }} = {\rm{ }}{Đ_{Ox}}\left( I \right).\)

Suy ra Ox là đường trung trực của II’ hay I’ đối xứng với I qua Ox

Do đó hai điểm I và I’ có cùng hoành độ và có tung độ đối nhau.

Vì vậy tọa độ điểm I’(–1; 2).

Gọi (C’) là ảnh của đường tròn (C) qua Đ_Ox.

Suy ra (C’) có tâm I’(–1; 2), bán kính \(R'{\rm{ }} = {\rm{ }}R{\rm{ }} = {\rm{ }}3.\)

Vậy phương trình đường tròn \(\left( {C'} \right):{\rm{ }}{\left( {x{\rm{ }} + {\rm{ }}1} \right)^2}\; + {\rm{ }}{\left( {y{\rm{ }}-{\rm{ }}2} \right)^2}\; = {\rm{ }}9.\)

Vận dụng 1

Cho hai điểm A, B là vị trí của hai nhà máy nằm cùng một phía bờ sông là đường thẳng d. Tìm trên bờ sông một địa điểm M để xây dựng một trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ trạm bơm về hai nhà máy là ngắn nhất (Hình 7).

Phương pháp giải:

Quan sát hình 7, suy luận để tìm chiều dài đường ống dẫn là ngắn nhất.

Lời giải chi tiết:

Gọi A’ là ảnh của A qua d.

Suy ra d là đường trung trực của đoạn thẳng AA’.

Mà \(M \in d\)  (giả thiết), do đó \(\;MA{\rm{ }} = {\rm{ }}MA'.\)

Vì AB cố định nên A’B cũng cố định.

Ta có \(MA{\rm{ }} + {\rm{ }}MB{\rm{ }} = {\rm{ }}MA'{\rm{ }} + {\rm{ }}MB{\rm{ }} \ge {\rm{ }}A'B\) (theo bất đẳng thức tam giác).

Suy ra MA + MB ngắn nhất khi và chỉ khi MA' + MB = A'B.

Tức là, ba điểm A’, M, B thẳng hàng hay M là giao điểm của A’B và d.

Vậy địa điểm M cần tìm là giao điểm của bờ sông (đường thẳng d) với đường thẳng A’B, trong đó A’ là ảnh của A qua d.