Giải mục 1 trang 46 Chuyên đề học tập Toán 11 - Kết nối tri thứcCho sơ đồ như trên Hình 2.28, ở đó A, B, C, D, E, F là các địa điểm nối với nhau bởi các con đường với độ dài của mỗi con đường được cho như trên hình. Quảng cáo
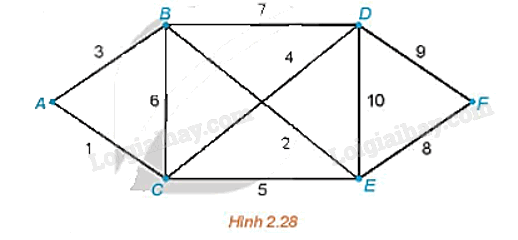
Đề bài Cho sơ đồ như trên Hình 2.28, ở đó A, B, C, D, E, F là các địa điểm nối với nhau bởi các con đường với độ dài của mỗi con đường được cho như trên hình. a) Hãy chỉ ra 2 đường đi từ A đến F và so sánh độ dài của hai đường đi đó. b) Với mỗi đỉnh V của sơ đồ trên Hình 2.28, ta gắn số I(V) là khoảng cách ngắn nhất để đi từ A đến V và gọi là nhãn vĩnh viễn của đỉnh V. Như vậy, ta có ngay I(A) = 0. Dựa vào Hình 2.28, hãy tìm các nhãn vĩnh viễn I(B), I(C) của hai đỉnh kề với A là B, C.
Phương pháp giải - Xem chi tiết Quan sát hình 2.28 để trả lời Lời giải chi tiết a) Hai đường đi từ A đến F, chẳng hạn là ABEF và ACEF. Độ dài của đường đi ABEF là AB + BE + EF = 3 + 2 + 8 = 13. Độ dài của đường đi ACEF là AC + CE + EF = 1 + 5 + 8 = 14. Do đó, đường đi ABEF có độ dài ngắn hơn đường đi ACEF. b) I(B) và I(C) lần lượt là các khoảng cách ngắn nhất để đi từ A đến B và C. Ta có I(B) = AB = 3, I(C) = AC = 1.
|




















Danh sách bình luận