Giải mục 1 trang 131, 132,133 SGK Toán 11 tập 1 - Cùng khám pháNhằm tìm hiểu tình hình học sinh rèn luyện sức khỏe qua môn bơi lội, nhà trường đề nghị mỗi lớp thống kê thời gian các bạn trong lớp dành cho môn thể thao này hàng tuần. Đầu tiên, Hùng- lớp trưởng lớp 11A1 - điều tra và ghi lại thời gian tập luyện và bơi lội của mỗi bạn. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Hoạt động Nhằm tìm hiểu tình hình học sinh rèn luyện sức khỏe qua môn bơi lội, nhà trường đề nghị mỗi lớp thống kê thời gian các bạn trong lớp dành cho môn thể thao này hàng tuần. Đầu tiên, Hùng- lớp trưởng lớp 11A1 - điều tra và ghi lại thời gian tập luyện và bơi lội của mỗi bạn. Nhưng sau đó, Hùng đã tập hợp số liệu trong bảng dưới đây ( Bảng 5.10):
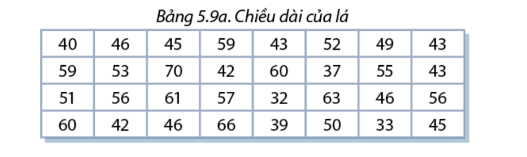
a, Tính thời gian tập luyện trung bình của 4 bạn ứng với nhóm ghép thứ nhất biết rằng số liệu Hùng ghi chép về 4 bạn này là 40, 35, 45, 55 (phút). Đặt \({c_1} = \frac{{30 + 60}}{2}\). Có nhận xét gì về chênh lệch kết quả tìm được với \({c_1}\). b, Nếu chỉ dựa vào Bảng 5.10 mà không có đầy đủ các số liệu lúc đầu , hãy thử đưa ra một cách ước tính thời gian bơi lội trung bình của lớp 11A1. Giải thích cách tính. Phương pháp giải: a, Thời gian tập luyện trung bình là số trung bình cộng của bốn số 40, 35, 45, 55. b, Tính số trung bình cộng của mỗi nhóm thời gian là \({c_1},{c_2},{c_3},{c_4},{c_5}\). Sau đó, lấy 5 số trung bình cộng nhân với tần số tương ứng và chia cho tổng tần số sẽ có thời gian bơi lội trung bình của lớp 11A1. Lời giải chi tiết: a, Thời gian tập luyện trung bình của 4 bạn nhóm ghép thứ nhất là: (40+35+45+55):4=43,75 ( phút) Ta có: \({c_1} = \frac{{30 + 60}}{2} = 45\) Nhận xét: Kết quả tìm được có giá trị gần bằng với \({c_1}\). b, Ta có: \({c_1} = \frac{{30 + 60}}{2} = 45\), \({c_2} = \frac{{60 + 90}}{2} = 75\), \({c_3} = \frac{{90 + 120}}{2} = 105\), \({c_4} = \frac{{120 + 150}}{2} = 135\), \({c_5} = \frac{{150 + 180}}{2} = 165\). Thời gian bơi lội trung bình của lớp 11A1 là:\(\frac{{{c_1}.4 + {c_2}.8 + {c_3}.12 + {c_4}.3 + {c_5}.5}}{{32}} = \frac{{45.4 + 75.8 + 105.12 + 135.3 + 165.5}}{{32}} = 102,18\)( phút) Ta đi tính các giá trị trung bình của từng nhóm thời gian là \({c_1},{c_2},{c_3},{c_4},{c_5}\) Sau đó, nhân 5 giá trị trung bình vừa tìm được với tần số tương ứng và chia cho tổng tần số để được thời gian bơi lội trung bình của cả lớp. Luyện tập Xét tình huống đã nêu ở đầu bài học a, Tính chiều dài trung bình của các lá cây được khảo sát trong mẫu số liệu ở Bảng 5.9 a. b, Ước tính chiều dài trung bình của lá cây thông qua mẫu số liệu ghép nhóm trong Bảng 5.9 b . Đối chiếu với kết quả ở câu a có nhận xét gì?
Phương pháp giải: a, Tính giá trị trung bình bằng cách cộng tổng các giá trị và chia cho tổng tần số b, Tính giá trị đại diện của từng nhóm và áp dụng công thức tính giá trị trung bình của bảng tần số ghép nhóm Lời giải chi tiết: a, Độ dài trung bình của lá cây là: ( 40+46+45+…+56+45):32=49,96 (cm) b, Bảng mẫu số liệu ghép nhóm
Ước tính độ dài trung bình của lá cây là: \(\mathop x\limits^\_ = \frac{{1620}}{{32}} = 50,625\) Kết quả câu b và a xấp xỉ nhau.
|























Danh sách bình luận