Giải đề thi giữa học kì 1 toán lớp 11 năm 2020 - 2021 trường THPT Xuân Phương

Đề bài

Mã đề 370

I. TRẮC NGHIỆM (6 điểm)

Câu 1. Có bao nhiêu số tự nhiên có 3 chữ số được tạo thành từ các số 0,1,2,3,4,5,6?

A. 180        B. 343         C. 210         D. 294

Câu 2. Giả sử phép đồng dạng với tỉ số 3 biến hai điểm M và N tương ứng thành M’, N’. Đẳng thức nào sau đây đúng?

A. $M'N' = 3MN$                  B. $MN = 3M'N'$

C. $MN = \dfrac{1}{9}M'N'$                   D. $M'N' = \dfrac{1}{3}MN$

Câu 3. Tất cả các nghiệm của phương trình $\cos x = \cos \alpha$ là

A. $x = \alpha  + k2\pi \left( {k \in \mathbb{Z}} \right)$     B. $x = \alpha  + k\pi \left( {k \in \mathbb{Z}} \right)$

C. $x =  \pm \alpha  + k\pi \left( {k \in \mathbb{Z}} \right)$        D. $x =  \pm \alpha  + k2\pi \left( {k \in \mathbb{Z}} \right)$

Câu 4. Tất cả các nghiệm của phương trình $\sin 2x - 2\cos x = 0$ là

A. $x = \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$    B. $x = \dfrac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)$

C. $x = \pi  + k2\pi \left( {k \in \mathbb{Z}} \right)$ D. $x = k\pi \left( {k \in \mathbb{Z}} \right)$

Câu 5. Trong 10.000 số nguyên dương đầu tiên có bao nhiêu số chứa đúng một chữ số 2, một chữ số 3, một chữ số 4?

A. 2401      B. 588         C. 168         D. 24

Câu 6. Điều kiện của tham số m để phương trình $\sqrt 2 \sin x + \left( {2m + 1} \right)\cos x = \sqrt 3$ có nghiệm là

A. $- 1 < m < 0$ B. $m <  - 1$       C. $\left[ \begin{array}{l}m \ge 0\\m \le  - 1\end{array} \right.$       D. $m > 0$

Câu 7. Một đội văn nghệ trường THPT Xuân Phương chuẩn bị được 3 vở kịch, 2 điệu múa và 5 bài hát. Tại hội diễn, mỗi đội chỉ được biểu diễn 1 trong các tiết mục vở kịch, điệu múa hoặc bài hát. Hỏi đội văn nghệ trên có bao nhiêu cách chọn chương trình biểu diễn, biết chất lượng các vở kịch, điệu múa, bài hát là như nhau.

A. 30          B. 20           C. 24           D. 10

Câu 8. Tập xác định của hàm số $y = \dfrac{{2\cos 2x - 1}}{{1 - \sin x}}$

A. $\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}$

B. $\mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}$

C. $\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}$

D. $\mathbb{R}\backslash \left\{ {\pi  + k2\pi ,k \in \mathbb{Z}} \right\}$

Câu 9. Giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y = 3\cos x - 1$

A. $\min y =  - 1,\max y = 2$

B. $\min y =  - 3,\max y =  - 1$

C. $\min y =  - 2,\max y = 4$

D. $\min y =  - 4,\max y = 2$

Câu 10. Trong mặt phẳng Oxy, cho $\overrightarrow v  = \left( {a;b} \right)$. Giả sử phép tịnh tiến theo $\overrightarrow v$ biến điểm M(x;y) thành điểm M’(x’;y’). Ta có biểu thức tọa độ của phép tịnh tiến theo vectơ $\overrightarrow v$ là:

A. $\left\{ \begin{array}{l}x' + b = x + a\\y' + a = y + b\end{array} \right.$

B. $\left\{ \begin{array}{l}x = x' + a\\y = y' + b\end{array} \right.$

C. $\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.$

D. $\left\{ \begin{array}{l}x' - b = x - a\\y' - a = y - b\end{array} \right.$

Câu 11. Tất cả các nghiệm của phương trình $\cot \left( {2{\rm{x}} + 10^\circ } \right) = \dfrac{1}{{\sqrt 3 }}$ là:

A. $x = 35^\circ  + k180^\circ \left( {k \in \mathbb{Z}} \right)$

B. $x = 25^\circ  + k90^\circ \left( {k \in \mathbb{Z}} \right)$

C. $x = 10^\circ  + k90^\circ \left( {k \in \mathbb{Z}} \right)$

D. $x = \dfrac{{5\pi }}{{36}} + \dfrac{{k\pi }}{3}\left( {k \in \mathbb{Z}} \right)$

Câu 12. Tập nghiệm của phương trình $\cos 3x =  - 1$ là:

A. $\left\{ {\dfrac{\pi }{3} + \dfrac{{k2\pi }}{3};k \in \mathbb{Z}} \right\}$

B. $\left\{ { - \dfrac{\pi }{6} + \dfrac{{k2\pi }}{3};k \in \mathbb{Z}} \right\}$

C. $\left\{ {\dfrac{\pi }{3} + k2\pi ;k \in \mathbb{Z}} \right\}$

D. $\left\{ {\dfrac{\pi }{6} + \dfrac{{k2\pi }}{3};k \in \mathbb{Z}} \right\}$

Câu 13. Phương trình $\tan x + \cot x - 2 = 0$ có bao nhiêu nghiệm thuộc khoảng $\left( { - \dfrac{\pi }{2};\pi } \right)$?

A. 2            B. 4             C. 1             D. 3

Câu 14. Nếu phép vi tự tỉ số $k\left( {k \ne 0} \right)$ biến hai điểm M, N lần lượt thành hai điểm M’, N’ thì

A. $\overrightarrow {M'N'}  = k\overrightarrow {MN}$ và $M'N' =  - kMN$

B. $\overrightarrow {M'N'}  = k\overrightarrow {MN}$ và $M'N' = \left| k \right|MN$

C. $\overrightarrow {M'N'}  = \left| k \right|\overrightarrow {MN}$ và $M'N' = kMN$

D. $\overrightarrow {M'N'} //\overrightarrow {MN}$ và $M'N' = \dfrac{1}{2}MN$

Câu 15. Một đội thanh niên tình nguyện có 14 người gồm 8 nam và 6 nữ. Hỏi có bao nhiêu cách phân công đội tình nguyện gồm 1 nam và 1 nữ về giúp đỡ các tỉnh miền Trung bị lũ lụt?

A. 14          B. 48           C. 40           D. 42

Câu 16. Phương trình $\sin 2x + \cos 2x =  - 1$ tương đương với phương trình nào sau đây?

A. $\sin \left( {2x + \dfrac{\pi }{4}} \right) =  - \dfrac{1}{2}$

B. $\sin \left( {2x + \dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 2 }}$

C. $\sin \left( {2x + \dfrac{\pi }{4}} \right) =  - \dfrac{1}{{\sqrt 2 }}$

D. $\sin \left( {2x + \dfrac{\pi }{4}} \right) = \dfrac{1}{2}$

Câu 17. Có thể lập được bao nhiêu vectơ (khác vectơ không) từ 20 điểm phân biệt cho trước?

A. 380        B. 40           C. 342         D. 400

Câu 18. Tập giá trị của hàm số $y = \cos x$ là:

A. $\left[ {0;1} \right]$      B. $\left( { - 1;1} \right)$       

C. $\left( {0;1} \right)$      D. $\left[ { - 1;1} \right]$

Câu 19. Tập xác định của hàm số $y = \tan x$ là

A. $D = \mathbb{R}\backslash \left\{ {k2\pi ,k \in \mathbb{Z}} \right\}$

B. $D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}$

C. $D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}$

D. $D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}$

Câu 20. Có bao nhiêu giá trị nguyên của tham số m để phương trình $\sin x = 2m - 3$ có nghiệm?

A. 2            B. 3             C. 1             D. Vô số

Câu 21. Từ thành phố A đến thành phố B có 6 con đường, từ thành phố B đến thành phố C có 4 con đường. Hỏi có bao nhiêu con đường đi từ A đến C và quay trở về qua B?

A. 20          B. 576         C. 144         D. 96

Câu 22. Trong mặt phẳng với hệ trục tọa độ Oxy, cho phép tịnh tiến theo $\overrightarrow v  = \left( {4;6} \right)$, phép tịnh tiến theo $\overrightarrow v$ biến $d:x + y + 1 = 0$ thành đường thẳng $d'$. Khi đó phương trình đường thẳng $d'$ là:

A. $- x + y + 9 = 0$     B. $x + y + 9 = 0$

C. $x - y + 9 = 0$          D. $x + y - 9 = 0$

Câu 23. Trong mặt phẳng Oxy, cho điểm $M\left( { - 1;3} \right)$. Hỏi M là ảnh của điểm nào qua phép vị tự tâm O, tỉ số $k =  - \dfrac{1}{2}$?

A. $A\left( {2;6} \right)$                           B. $A\left( {2; - 6} \right)$    

C. $A\left( { - 2; - 6} \right)$           D. $A\left( { - 2;6} \right)$

Câu 24. Trong mặt phẳng tọa độ Oxy, cho phép dời hình biến điểm $A\left( {1; - 2} \right)$ thành $A'$ và biến điểm $B\left( {0;3} \right)$ thành $B'$. Khi đó độ dài $A'B'$ là:

A. $A'B' = \sqrt {26}$ B. $A'B' = \sqrt {16}$

C. $A'B' = \sqrt {24}$ D. $A'B' = \sqrt 2$

Câu 25. Phương trình nào sau đây vô nghiệm?

A. $\cot {\rm{x}} = \sqrt 2$  B. $\cos x = \dfrac{2}{3}$

C. $\cos x = \sqrt 3$     D. $\sin 2{\rm{x}} =  - \dfrac{{\sqrt 2 }}{2}$

Câu 26. Tổ 1 của lớp 11A có 8 học sinh nam và 4 học sinh nữ. Thầy giáo muốn chọn ra 1 học sinh làm tổ trưởng. Hỏi thầy có bao nhiêu cách chọn?

A. 32          B. 12           C. 24           D. 28

Câu 27. Trong mặt phẳng Oxy, cho điểm $A(0;5)$. Tìm tọa độ ảnh A’ của điểm A qua phép quay tâm O góc quay $90^\circ$.

A. $A'\left( {5; - 5} \right)$             B. $A'\left( {5;0} \right)$      

C. $A'\left( { - 5;0} \right)$              D. $A'\left( {0; - 5} \right)$

Câu 28. Tất cả các nghiệm của phương trình $2{\cos ^2}x - \sqrt 3 \sin 2x = 3$ là:

A. $x = \dfrac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)$

B. $x =  - \dfrac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)$

C. $x = \dfrac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)$

D. $x =  - \dfrac{\pi }{6} + k2\pi \left( {k \in \mathbb{Z}} \right)$

Câu 29. Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc quay $\alpha ,0 < \alpha  \le 2\pi$ biến hình vuông thành chính nó?

A. Bốn        B. Một        C. Ba          D. Hai

Câu 30. Số vị trí biểu diễn nghiệm của phương trình $\sin \left( {x - \dfrac{{2\pi }}{3}} \right) = \dfrac{1}{2}$ trên đường tròn lượng giác là

A. 1             B. 6             C. 4             D. 2

II. TỰ LUẬN (4 điểm)

Câu 31. (1,5 điểm) Giải các phương trình sau

a. $4{\cos ^2}x + 8\cos x + 3 = 0$

b. $\dfrac{{\sqrt 3 \cos x + \sin x}}{{2\cos x - 1}} = 0$

Câu 32. (1 điểm ) Tính tổng các nghiệm của phương trình $1 - \sqrt 3 \tan \left( {3x - \dfrac{\pi }{4}} \right) = 0$ với $\dfrac{\pi }{6} < x < \dfrac{\pi }{2}$

Câu 33.(1,5 điểm) Tìm m để phương trình $\left( {1 - \sin x} \right)\left( {\cos 8x + m\sin x} \right) = m{\cos ^2}x$ có đúng 4 nghiệm $x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{2}} \right]$.

Câu 34.(0,5 điểm) Từ các số 0;1;2;5;6;9 có thể lập được bao nhiêu số tự nhiên lẻ, có 4 chữ số khác nhau?

Câu 35.(0,5 điểm) Trong mặt phẳng tọa độ Oxy, cho đường tròn $\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4$. Tìm ảnh $\left( {C'} \right)$ của $\left( C \right)$ qua phép vị tự tâm $O$ tỉ số $k = 3$.

Lời giải chi tiết

PHẦN I. TRẮC NGHIỆM

1. D	2.A	3. D	4. A	5. C
6. C	7. D	8. C	9. D	10. C
11. B	12.A	13.C	14.B	15.B
16.C	17.A	18.D	19. D	20.A
21.D	22.D	23.B	24.A	25.C
26.B	27C	28.B	29.A	30.D

 

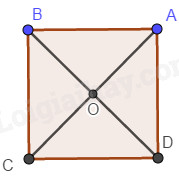
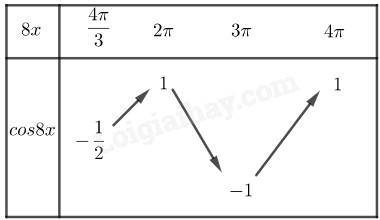
Câu 1. (TH)

Phương pháp

Số có 3 chữ số có dạng $\overline {abc}$.

Số a luôn khác 0.

Cách giải

Gọi số có 3 chữ số là $\overline {abc}$. Ta chọn a trước.

Có 6 cách chọn a, do $a \in \left\{ {1;2;3;4;5;6} \right\}$

Có 7 cách chọn b, do $b \in \left\{ {0;1;2;3;4;5;6} \right\}$

Có 7 cách chọn c, do $c \in \left\{ {0;1;2;3;4;5;6} \right\}$

Theo quy tắc nhân: Có 6.7.7=294 cách chọn

Câu 2. (NB)

Phương pháp

Phép đồng dạng tỉ số k biến M, N lần lượt thành M’, N’ thì $MN = k.M'N'$.

Cách giải

Phép đồng dạng tỉ số 3 biến M, N lần lượt thành M’, N’ thì $MN = 3M'N'$

Câu 3. (NB)

Phương pháp

$\cos x = \cos \alpha$ $\Leftrightarrow \left[ \begin{array}{l}x = \alpha  + k2\pi \\x =  - \alpha  + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)$

Cách giải

$\cos x = \cos \alpha$ $\Leftrightarrow \left[ \begin{array}{l}x = \alpha  + k2\pi \\x =  - \alpha  + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)$

Nên tất cả các nghiệm của phương trình $\cos x = \cos \alpha$ là $x =  \pm \alpha  + k2\pi ,k \in \mathbb{Z}$.

Câu 4. (TH)

Phương pháp

 Đưa về phương trình lượng giác cơ bản.

$\cos x = \cos \alpha$ $\Leftrightarrow \left[ \begin{array}{l}x = \alpha  + k2\pi \\x =  - \alpha  + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)$

$\sin x = \sin \alpha  \Leftrightarrow \left[ \begin{array}{l}x = \alpha  + k2\pi \\x = \pi  - \alpha  + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)$

Cách giải

Ta có $\sin 2x - 2\cos x = 0$$\Leftrightarrow 2\sin x\cos x - 2\cos x = 0$

$\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}\cos x = 0\\\sin x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x = \dfrac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)\end{array}$

Câu 5.(VD)

Phương pháp

Số tự nhiên nhỏ hơn 10000 có không quá 4 chữ số, mà trong đó có chữ số 2, 3, 4 nên số cần tìm có 3 hoặc 4 chữ số.

Cách giải

Gọi số cần tìm là $\overline {abcd}$, nếu $a = 0$ thì số này có 3 chữ số, nếu $a \ne 0$ thì số có 4 chữ số.

Có $A_4^3$ cách xếp vị trí của 2, 3, 4 vào 4 vị trí trên. Vị trí còn lại có 7 cách chọn là 0;1;5;6;7;8;9. Theo quy tắc nhân, ta có $A_4^3.7 = 168$ số tự nhiên thỏa mãn bài toán.

Câu 6. (TH)

Phương pháp

Phương trình $a\sin x + b\cos x = c$ có nghiệm $\Leftrightarrow {c^2} \le {a^2} + {b^2}$

Cách giải

 Phương trình $\sqrt 2 \sin x + \left( {2m + 1} \right)\cos x = \sqrt 3$ có nghiệm $\Leftrightarrow 3 \le 2 + {\left( {2m + 1} \right)^2} \Leftrightarrow \left[ \begin{array}{l}m \ge 0\\m \le  - 1\end{array} \right.$

Câu 7.(TH)

Phương pháp

Tìm tổng các tiết mục văn nghệ. Tìm số cách chọn một tiết mục trong tổng các tiết mục.

Cách giải

Có 3+2+5=10 tiết mục nên có 10 cách chọn 1 tiết mục.

Câu 8. (TH)

Phương pháp

Hàm số $y = \dfrac{{f\left( x \right)}}{{g\left( x \right)}}$ xác định khi và chỉ khi $g\left( x \right) \ne 0$.

Cách giải

Điều kiện: $1 - \sin x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)$

TXĐ: $D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k2\pi ,k \in \mathbb{Z}} \right\}$

Câu 9. (TH)

Phương pháp

Sử dụng tính chất: $- 1 \le \cos x \le 1\forall x \in \mathbb{R}$ rồi biến đổi hàm số để tìm GTLN, GTNN.

Cách giải

TXĐ: $D = \mathbb{R}$.

$\begin{array}{l} - 1 \le \cos x \le 1 \Rightarrow  - 3 \le 3\cos x \le 3\\ \Leftrightarrow  - 4 \le y \le 2\end{array}$

$\Rightarrow \min y =  - 4;\max y = 2$

Câu 10. (NB)

Phương pháp

${T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'}  = \overrightarrow v$

Cách giải

${T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'}  = \overrightarrow v$$\Leftrightarrow \left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.$

Câu 11.(TH)

Phương pháp

Tập xác định của hàm số $y = \cot x$ là $D = \mathbb{R}\backslash \left\{ {k.180^\circ ,k \in \mathbb{Z}} \right\}$.

$\cot x = \cot \alpha  \Leftrightarrow x = \alpha  + k\pi \left( {k \in \mathbb{Z}} \right)$

Cách giải

Tập xác định: $D = \mathbb{R}\backslash \left\{ { - 5^\circ  + k.90^\circ ,k \in \mathbb{Z}} \right\}$

$\begin{array}{l}\cot \left( {2x + 10^\circ } \right) = \cot 60^\circ \\ \Leftrightarrow 2x + 10^\circ  = 60^\circ  + k.180^\circ \left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow x = 25^\circ  + k.90^\circ \left( {k \in \mathbb{Z}} \right)\end{array}$

Câu 12. (TH)

Phương pháp

$\cos x =  - 1 \Leftrightarrow x = \pi  + k2\pi \left( {k \in \mathbb{Z}} \right)$

Cách giải

$\begin{array}{l}\cos 3x =  - 1 \Leftrightarrow 3x = \pi  + k2\pi \\ \Leftrightarrow x = \dfrac{\pi }{3} + \dfrac{{k2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\end{array}$

Câu 13. (VD)

Phương pháp

B1: Tìm tập xác định

B2: Sử dụng công thức $\cot x = \dfrac{1}{{\tan x}}$ rồi đưa vể phương trình bậc hai đối với tan.

B3: Giải phương trình tìm tanx rồi tìm x.

Cách giải

TXĐ: $D = \mathbb{R}\backslash \left\{ {\dfrac{{k\pi }}{2},k \in \mathbb{Z}} \right\}$

$\tan x + \cot x - 2 = 0$

$\begin{array}{l} \Leftrightarrow \dfrac{{{{\left( {\tan x - 1} \right)}^2}}}{{\tan x}} = 0 \Leftrightarrow \tan x = 1\\ \Leftrightarrow x = \dfrac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)\end{array}$

Mà $x \in \left( { - \dfrac{\pi }{2};\pi } \right)$

$\begin{array}{l} \Rightarrow  - \dfrac{\pi }{2} < \dfrac{\pi }{4} + k\pi  < \pi \\ \Leftrightarrow  - \dfrac{3}{4} < k < \dfrac{3}{4} \Rightarrow k = 0\end{array}$

Vậy phương trình có 1 nghiệm trong $\left( { - \dfrac{\pi }{2};\pi } \right)$

Câu 14.(NB)

Phương pháp

Phép vi tự tỉ số $k\left( {k \ne 0} \right)$ biến hai điểm M, N lần lượt thành hai điểm M’, N’ thì $\overrightarrow {M'N'}  = k\overrightarrow {MN} ;M'N' = \left| k \right|MN$.

Cách giải

Phép vi tự tỉ số $k\left( {k \ne 0} \right)$ biến hai điểm M, N lần lượt thành hai điểm M’, N’ thì $\overrightarrow {M'N'}  = k\overrightarrow {MN} ;M'N' = \left| k \right|MN$.

Câu 15. (TH)

Phương pháp

Tính số cách chọn 1 nam và số cách chọn 1 nữ.

Sử dụng quy tắc nhân.

Cách giải

Có 8 cách chọn 1 nam và 6 cách chọn 1 nữ. Theo quy tắc nhân ta có 48 cách phân công đội tình nguyện gồm 1 nam và một nữ.

Câu 16.(TH)

Phương pháp

$\begin{array}{l}{\rm{a}}\sin x + b\cos x = c\left( {{c^2} \le {a^2} + {b^2}} \right)\\ \Leftrightarrow \sin \left( {x + \alpha } \right) = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\end{array}$

Cách giải

$\sin 2x + \cos 2x =  - 1$

$\Leftrightarrow \dfrac{1}{{\sqrt 2 }}\sin 2x + \dfrac{1}{{\sqrt 2 }}\cos 2x =  - \dfrac{1}{{\sqrt 2 }}$

$\Leftrightarrow \sin \left( {2x + \dfrac{\pi }{4}} \right) =  - \dfrac{1}{{\sqrt 2 }}$

Câu 17.(TH)

Phương pháp

Sử dụng chỉnh hợp chập k của tập n phần tử: $A_n^k = \dfrac{{n!}}{{\left( {n - k} \right)!}}$

Cách giải

Một cặp sắp thứ tự gồm 2 điểm $\left( {A,B} \right)$ cho ta một vectơ có điểm đầu A, điểm cuối B và ngược lại. Như vậy, mỗi vectơ có thể xem là một chỉnh hợp chập 2 của tập 20 phần tử đã cho.

Số vectơ cần tìm là: $A_{20}^2 = 380$

Câu 18.(NB)

Phương pháp

Sử dụng tính chất của hàm $y = \cos x$

Cách giải

Tập giá trị của hàm số $y = \cos x$ là $\left[ { - 1;1} \right]$.

Câu 19.(NB)

Phương pháp

Điều kiện xác định của $\tan x$ là $x \ne \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$

Cách giải

Điều kiện xác định của $\tan x$ là :

$\cos x \ne 0 \Leftrightarrow$ $x \ne \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$

$\Rightarrow$TXĐ: $D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}$

Câu 20.(TH)

Phương pháp

$\sin x = a$ có nghiệm $\Leftrightarrow  - 1 \le a \le 1$

Cách giải

$\sin x = 2m - 3$ có nghiệm $\Leftrightarrow  - 1 \le 2m - 3 \le 1 \Leftrightarrow 1 \le m \le 2$

$\Rightarrow m \in \left\{ {1;2} \right\}$ hay m có 2 giá trị.

Câu 21.

Phương pháp

Sử dụng quy tắc nhân

Cách giải

Có 6 con đường đi từ A đến B, 4 con đường từ B đến C nên có 6.4=24 con đường từ A đến C. Có 4 con đường từ C đến B.

Vậy có 24.4=96 con đường thỏa mãn yêu cầu bài toán.

Câu 22.(VD)

Phương pháp

Biểu diễn tọa độ của M theo M’ rồi thay và phương trình của d tìm d’.

${T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'}  = \overrightarrow v$$\Leftrightarrow \left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.$

Cách giải

${T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \overrightarrow {MM'}  = \overrightarrow v$$\Leftrightarrow \left\{ \begin{array}{l}x' = x + 4\\y' = y + 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = x' - 4\\y = y' - 6\end{array} \right.$. Thay vào phương trình của d ta được:

$\begin{array}{l}\left( {x' - 4} \right) + \left( {y' - 6} \right) + 1 = 0\\ \Leftrightarrow x' + y' - 9 = 0\end{array}$

Vậy $d':x + y - 9 = 0$

Câu 23.(VD)

Phương pháp

Phép vị tự tâm O tỉ số k: ${V_{\left( {O;k} \right)}}\left( A \right) = M \Leftrightarrow \overrightarrow {OM}  = k\overrightarrow {{\rm{O}}A}$

Cách giải

Giả sử M là ảnh của A qua phép vị tự tâm O tỉ số $- \dfrac{1}{2}$. Khi đó, ta có:

$\begin{array}{l}{V_{\left( {O; - \dfrac{1}{2}} \right)}}\left( A \right) = M \Leftrightarrow \overrightarrow {OM}  =  - \dfrac{1}{2}\overrightarrow {OA} \\ \Leftrightarrow \overrightarrow {OA}  =  - 2\overrightarrow {OM} \\ \Leftrightarrow \left\{ \begin{array}{l}{x_A} =  - 2{x_M} = 2\\{y_A} =  - 2{y_M} =  - 6\end{array} \right. \Rightarrow A\left( {2; - 6} \right)\end{array}$

Câu 24.

Phương pháp

Sử dụng tính chất: Phép dời hình bảo toàn khoảng cách.

Cách giải

Phép dời hình biến điểm $A\left( {1; - 2} \right)$ thành $A'$ và biến điểm $B\left( {0;3} \right)$ thành $B'$. Khi đó độ dài $A'B' = AB = \sqrt {{{\left( {{x_B} - {x_B}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}}  = \sqrt {26}$.

Câu 25. (NB)

Phương pháp

$\cos x = a$ vô nghiệm $\Leftrightarrow \left| a \right| > 1$

Cách giải

$\sqrt 3  > 1 \Rightarrow \cos x = \sqrt 3$ vô nghiệm.

Câu 26.(TH)

Phương pháp

Sử dụng quy tắc cộng.

Cách giải

Có 2 phương án chọn. Phương án thứ nhất là chọn học sinh nam, có 8 cách. Phương án thứ hai là chọn học sinh nữ, có 4 cách chọn. Vậy có 12 cách chọn tổ trưởng.

Câu 27. (TH)

Phương pháp

Phép quay ${Q_{\left( {O;90^\circ } \right)}}\left( {M\left( {x;y} \right)} \right) = M'\left( { - y;x} \right)\forall x,y$

Cách giải

${Q_{\left( {O;90^\circ } \right)}}\left[ {A\left( {0;5} \right)} \right] = A'\left( { - 5;0} \right)$

Câu 28. Tất cả các nghiệm của phương trình $2{\cos ^2}x - \sqrt 3 \sin 2x = 3$ là:

A. $x = \dfrac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)$

B. $x =  - \dfrac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)$

C. $x = \dfrac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)$

D. $x =  - \dfrac{\pi }{6} + k2\pi \left( {k \in \mathbb{Z}} \right)$

Phương pháp

Đưa về phương trình bậc nhất của $\sin$ và cos bằng cách hạ bậc.

Công thức hạ bậc ${\cos ^2}x = \dfrac{{\cos 2x + 1}}{2}$.

Giải phương trình bậc nhất đối với sin và cos:

$\begin{array}{l}a\cos x + b\sin x = c\left( {{c^2} \le {a^2} + {b^2}} \right)\\ \Leftrightarrow \dfrac{a}{{\sqrt {{a^2} + {b^2}} }}\cos x + \dfrac{b}{{\sqrt {{a^2} + {b^2}} }}\sin x = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\\ \Leftrightarrow \sin \left( {x + \alpha } \right) = \dfrac{c}{{\sqrt {{a^2} + {b^2}} }}\end{array}$

$\left( {\sin \alpha  = \dfrac{a}{{\sqrt {{a^2} + {b^2}} }};\cos \alpha  = \dfrac{b}{{\sqrt {{a^2} + {b^2}} }}} \right)$

Cách giải

$2{\cos ^2}x - \sqrt 3 \sin 2x = 3$

$\begin{array}{l} \Leftrightarrow \cos 2x - \sqrt 3 \sin 2x = 2\\ \Leftrightarrow \dfrac{1}{2}\cos 2x - \dfrac{{\sqrt 3 }}{2}\sin 2x = 1\\ \Leftrightarrow \sin \left( {\dfrac{\pi }{6} - 2x} \right) = 1\\ \Leftrightarrow \dfrac{\pi }{6} - 2x = \dfrac{\pi }{2} + k2\pi \\ \Leftrightarrow x =  - \dfrac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)\end{array}$

Câu 29. (VDC)

Phương pháp

Phép quay biến hình vuông thành chính nó khi và chỉ khi phép quay biến đỉnh thành đỉnh.

Cách giải

Phép quay biến hình vuông thành chính nó khi và chỉ khi phép quay biến đỉnh thành đỉnh.

Giả sử hình vuông đó là ABCD với vị trí các điểm A, B, C, D như hình sau:

 

Phép quay tâm O biến ABCD thành ABCD là  ${Q_{\left( {O,2\pi } \right)}}$.

Phép quay tâm O biến ABCD thành BCDA là ${Q_{\left( {O;\frac{\pi }{2}} \right)}}$

Phép quay tâm O biến ABCD thành CDAB là ${Q_{\left( {O,\pi } \right)}}$

Phép quay tâm O biến ABCD thành DABC là ${Q_{\left( {O,\frac{{3\pi }}{2}} \right)}}$

Vì hình vuông đề cho không phân biệt thứ tự các điểm nên có tất cả 4 phép quay biến hình vuông thành chính nó.

Câu 30. (TH)

Phương pháp

Giải phương trình rồi xác định vị trí các họ nghiệm trên đường tròn lượng giác.

$\sin x = \sin a \Leftrightarrow \left[ \begin{array}{l}x = a + k2\pi \\x = \pi  - a + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)$

Cách giải

$\begin{array}{l}\sin \left( {x - \dfrac{{2\pi }}{3}} \right) = \dfrac{1}{2}\\ \Leftrightarrow \left[ \begin{array}{l}x - \dfrac{{2\pi }}{3} = \dfrac{\pi }{6} + k2\pi \\x - \dfrac{{2\pi }}{3} = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{5\pi }}{6} + k2\pi \\x = \dfrac{{3\pi }}{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}$

Có 2 vị trí biểu diễn nghiệm trên đường tròn lượng giác.

II. PHẦN TỰ LUẬN (4 điểm)

Câu 31. (VD) Giải các phương trình sau

a. $4{\cos ^2}x + 8\cos x + 3 = 0$

b. $\dfrac{{\sqrt 3 \cos x + \sin x}}{{2\cos x - 1}} = 0$

Phương pháp

a.

Đặt $t = \cos x\left( {\left| t \right| \le 1} \right)$, đưa phương trình ban đầu thành phương trình bậc 2 ẩn t.

Thay các giá trị t tìm được để tìm x.

b.

B1: Tìm TXĐ

B2: $\dfrac{{f\left( x \right)}}{{g\left( x \right)}} = 0 \Leftrightarrow f\left( x \right) = 0$

Cách giải

a. Đặt $t = \cos x\left( {\left| t \right| \le 1} \right)$, phương trình trở thành

$4{t^2} + 8t + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t =  - \dfrac{1}{2}\\t =  - \dfrac{3}{2}(L)\end{array} \right.$

$\Leftrightarrow \cos x =  - \dfrac{1}{2} \Leftrightarrow x =  \pm \dfrac{{2\pi }}{3} + k2\pi$$\left( {k \in \mathbb{Z}} \right)$.

b.

Điều kiện: $2\cos x - 1 \ne 0 \Leftrightarrow x \ne  \pm \dfrac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)$

$\dfrac{{\sqrt 3 \cos x + \sin x}}{{2\cos x - 1}} = 0$

$\begin{array}{l} \Leftrightarrow \sqrt 3 c{\rm{osx}} + {\mathop{\rm s}\nolimits} {\rm{inx}} = 0 \Leftrightarrow \sin \left( {x + \dfrac{\pi }{3}} \right) = 0\\ \Leftrightarrow x + \dfrac{\pi }{3} = k\pi  \Leftrightarrow x =  - \dfrac{\pi }{3} + k\pi ,k \in \mathbb{Z}\end{array}$

Kết hợp với điều kiện $x \ne  \pm \dfrac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)$, ta được $x = \dfrac{{2\pi }}{3} + k2\pi$$\left( {k \in \mathbb{Z}} \right)$.

Câu 32. (VD) Tính tổng các nghiệm của phương trình $1 - \sqrt 3 \tan \left( {3x - \dfrac{\pi }{4}} \right) = 0$ với $\dfrac{\pi }{6} < x < \dfrac{\pi }{2}$

Phương pháp

B1: Tìm TXĐ $\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$

B2: $\tan x = a \Leftrightarrow x = \arctan a + k\pi ,k \in \mathbb{Z}$.

B3: Thay họ nghiệm của phương trình vào $\dfrac{\pi }{6} < x < \dfrac{\pi }{2}$ tìm k.

B4: Với mỗi giá trị k tìm được ta được 1 nghiệm của phương trình.

Cách giải

TXĐ: $x \ne \dfrac{\pi }{4} + \dfrac{{k\pi }}{3}\left( {k \in \mathbb{Z}} \right)$

$1 - \sqrt 3 \tan \left( {3x - \dfrac{\pi }{4}} \right) = 0$$\Leftrightarrow \tan \left( {3{\rm{x}} - \dfrac{\pi }{4}} \right) = \dfrac{1}{{\sqrt 3 }}$$\Leftrightarrow 3x - \dfrac{\pi }{4} = \dfrac{\pi }{6} + k\pi  \Leftrightarrow x = \dfrac{{5\pi }}{{36}} + \dfrac{{k\pi }}{3}$

Do $\dfrac{\pi }{6} < x < \dfrac{\pi }{2}$ nên

$\begin{array}{l}\dfrac{\pi }{6} < \dfrac{{5\pi }}{{36}} + \dfrac{{k\pi }}{3} < \dfrac{\pi }{2}\\ \Leftrightarrow \dfrac{1}{{12}} < k < \dfrac{{13}}{{12}} \Rightarrow k = 1\end{array}$

Vậy $x = \dfrac{{5\pi }}{{36}} + \dfrac{\pi }{3} = \dfrac{{17\pi }}{{36}}$

Tổng các nghiệm là $\dfrac{{17\pi }}{{36}}$

Câu 33.(VDC) Tìm m để phương trình $\left( {1 - \sin x} \right)\left( {\cos 8x + m\sin x} \right) = m{\cos ^2}x$ có đúng 4 nghiệm $x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{2}} \right]$.

Phương pháp

Sử dụng công thức ${\cos ^2}x = 1 - {\sin ^2}x$.

Giải nghiệm tìm x rồi sử dụng bảng biến thiên của hàm số $y = \cos x$ để biện luận số nghiệm phương trình còn lại.

Cách giải

$\begin{array}{l}\left( {1 - \sin x} \right)\left( {\cos 8x + m\sin x} \right) = m{\cos ^2}x\\ \Leftrightarrow \left( {1 - \sin x} \right)\left( {\cos 8x + m\sin x} \right)\\ = m\left( {1 - \sin x} \right)\left( {1 + \sin x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\sin x = 1\\\cos 8x + m\sin x = m + m\sin x\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{2}} \right]\\\cos 8x = m(2)\end{array} \right.\end{array}$

(1) có 4 nghiệm phân biệt $x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{2}} \right]$ khi và chỉ khi (2) có đúng 3 nghiệm phân biệt $x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{2}} \right)$

Xét hàm số $y = \cos 8x$ trên $\left[ {\dfrac{\pi }{6};\dfrac{\pi }{2}} \right)$. Khi đó nghiệm của (2) là hoành độ giao điểm của hàm số này và đường thẳng $y = m$.

$x \in \left[ {\dfrac{\pi }{6};\dfrac{\pi }{2}} \right) \Rightarrow 8x \in \left[ {\dfrac{{4\pi }}{3};4\pi } \right)$

Bảng biến thiên:

 

Từ bảng biến thiên ta có đường thẳng $y = m$ cắt đồ thị hàm số $y = \cos 8x$ tại 3 điểm phân biệt khi và chỉ khi $- \dfrac{1}{2} \le m < 1$.

Vậy $- \dfrac{1}{2} \le m < 1$.

Câu 34.(VD) Từ các số 0;1;2;5;6;9 có thể lập được bao nhiêu số tự nhiên lẻ, có 4 chữ số khác nhau?

Phương pháp

Gọi số cần tìm là $\overline {abcd}$

Số cần tìm là số lẻ nên ta tính số cách chọn d trước.

Tính số cách chọn $a,b,c\left( {a \ne 0} \right)$ rồi sử dụng quy tắc nhân để tính số các số thỏa mãn yêu cầu bài toán.

Cách giải

Gọi số cần tìm là $\overline {abcd}$

$\Rightarrow d \in \left\{ {1;5;9} \right\}$. Có 3 cách chọn d.

Có 4 cách chọn a.

Có 4 cách chọn b.

Có 3 cách chọn c.

Theo qui tắc nhân: Có 144 số thỏa mãn yêu cầu bài toán.

Câu 35.(VD) Trong mặt phẳng tọa độ Oxy, cho đường tròn $\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4$. Tìm ảnh $\left( {C'} \right)$ của $\left( C \right)$ qua phép vị tự tâm $O$ tỉ số $k = 3$.

Phương pháp

Ảnh của đường tròn tâm I bán kính R qua phép vị tự tâm O, tỉ số k là đường tròn tâm I’ bán kính R’ thỏa mãn:

$\left\{ \begin{array}{l}\overrightarrow {OI'}  = k\overrightarrow {{\rm{O}}I} \\R' = \left| k \right|{\rm{R}}\end{array} \right.$

Cách giải

Đường tròn (C) có tâm I(1;1) bán kính R=2. Gọi I’,R’ lần lượt là tâm và bán kính đường tròn (C’).

$\Rightarrow \left\{ \begin{array}{l}\overrightarrow {OI'}  = k\overrightarrow {{\rm{O}}I} \\R' = \left| k \right|{\rm{R}}\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}I'\left( {3;3} \right)\\R' = 6\end{array} \right.$

Vậy đường tròn (C’): ${\left( {x - 3} \right)^2} + {\left( {y - 3} \right)^2} = 36$.

 Loigiaihay.com