Giải bài 9.67 trang 69 sách bài tập toán 8 - Kết nối tri thức với cuộc sống

Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N, P lần lượt là trung điểm của HA, HB, HC. Chứng minh rằng:

Tổng hợp đề thi giữa kì 1 lớp 8 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên

Quảng cáo

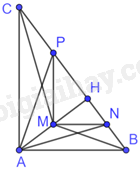
Đề bài

Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N, P lần lượt là trung điểm của HA, HB, HC. Chứng minh rằng:

a) $\Delta MNP\backsim \Delta ABC$ và tìm tỉ số đồng dạng

b) $\Delta ABN\backsim \Delta CAM$ và $\Delta ACP\backsim \Delta BAM$

c) $AN \bot CM$ và $AP \bot BM$

Phương pháp giải - Xem chi tiết

a) Sử dụng kiến thức về trường hợp đồng dạng của tam giác để chứng minh tam giác đồng dạng: Trường hợp đồng dạng cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.

b) Sử dụng kiến thức về trường hợp đồng dạng của tam giác để chứng minh tam giác đồng dạng:

+ Trường hợp đồng dạng cạnh – góc – cạnh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.

+ Trường hợp đồng dạng góc – góc: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

c) Sử dụng kiến thức về 3 đường cao trong tam giác: 3 đường cao trong tam giác đồng quy tại một điểm, điểm đó được gọi là trực tâm của tam giác.

Lời giải chi tiết

a) Tam giác CAH có P, M lần lượt là trung điểm của CH, AH nên MP là đường trung bình của tam giác ACH, suy ra $\frac{{MP}}{{AC}} = \frac{1}{2}$

Tam giác BAH có N, M lần lượt là trung điểm của BH, AH nên MN là đường trung bình của tam giác ABH, suy ra $\frac{{MN}}{{AB}} = \frac{1}{2}$

Ta có: $\frac{{PN}}{{CB}} = \frac{{PH + HN}}{{CH + HB}} = \frac{{PH + HN}}{{2\left( {PH + HN} \right)}} = \frac{1}{2}$

Tam giác MNP và tam giác ABC có:

$\frac{{MP}}{{AC}} = \frac{{PN}}{{CB}} = \frac{{MN}}{{AB}} = \frac{1}{2}$ nên $\Delta MNP\backsim \Delta ABC\left( c-c-c \right)$ với tỉ số đồng dạng bằng $\frac{1}{2}$

b) Tam giác ABC vuông tại A nên $\widehat {BAC} = {90^0}$

Vì AH là đường cao trong tam giác ABC nên $AH \bot BC$. Do đó, $\widehat {AHB} = \widehat {AHC} = {90^0}$

Tam giác ABH và tam giác HAC có:

$\widehat {AHB} = \widehat {AHC} = {90^0},\widehat {ABH} = \widehat {CAH}\left( { = {{90}^0} - \widehat {ACH}} \right)$

Do đó, $\Delta HBA\backsim \Delta HAC\left( g-g \right)$. Suy ra: $\frac{{AB}}{{AC}} = \frac{{BH}}{{AH}} = \frac{{BN}}{{MA}}$

Tam giác ABN và tam giác CAM có:

$\widehat {ABN} = \widehat {CAM}\left( {cmt} \right),\frac{{AB}}{{AC}} = \frac{{BN}}{{MA}}\left( {cmt} \right)$

Do đó, $\Delta ABN\backsim \Delta CAM\left( c-g-c \right)$

Vì $\Delta HBA\backsim \Delta HAC\left( g-g \right)$. Suy ra: $\frac{{AB}}{{AC}} = \frac{{AH}}{{CH}} = \frac{{AM}}{{CP}}$

Tam giác ACP và tam giác BAM có:

$\widehat {ACP} = \widehat {MAB}\left( { = {{90}^0} - \widehat {CAH}} \right),\frac{{AB}}{{AC}} = \frac{{AM}}{{CP}}\left( {cmt} \right)$

Do đó, $\Delta ACP\backsim \Delta BAM\left( c-g-c \right)$

c) Vì MN là đường trung bình trong tam giác AHB nên MN//AB, mà $AB \bot AC$ nên $MN \bot AC$

Trong tam giác CAN có: $MN \bot AC$ nên MN là đường cao trong tam giác CAN, AH là đường cao trong tam giác CAN, mà M là giao điểm của MN và AH nên M là trực tâm trong tam giác CAN. Vậy $CM \bot AN$

Vì MP là đường trung bình trong tam giác CAH nên MP//AC, mà $AB \bot AC$ nên $MP \bot AB$

Trong tam giác PAB có: $MP \bot AB$ nên MP là đường cao trong tam giác PAB, AH là đường cao trong tam giác PAB, mà M là giao điểm của MP và AH nên M là trực tâm trong tam giác PAB. Vậy $AP \bot BM$