Giải Bài 95 trang 97 sách bài tập toán 7 - Cánh diều

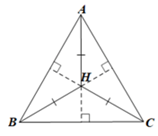
Đề bài

Cho tam giác ABC có trực tâm H đồng thời cũng là điểm cách đều ba đỉnh của tam giác. Tính số đo các góc của tam giác ABC.

Lời giải chi tiết

 

Gọi M là giao điểm của AH và BC.

Vì H cách đều ba đỉnh của tam giác ABC nên HA = HB = HC.

Do HB = HC nên H nằm trên đường trung trực của đoạn thẳng BC.

Tam giác ABC có trực tâm H nên AH ⊥ BC tại M.

Do đó AH là đường trung trực của BC và M là trung điểm của BC.

Khi đó MB = MC.

Xét ∆ABM và ∆ACM có:

\(\widehat {AMB} = \widehat {AMC}\left( { = 90^\circ } \right)\)

AM là cạnh chung,

MB = MC (chứng minh trên).

Do đó ∆ABM = ∆ACM (hai cạnh góc vuông)

Suy ra AB = AC (hai cạnh tương ứng).

Chứng minh tương tự ta cũng có: AB = BC.

Do đó AB = BC = AC nên tam giác ABC là tam giác đều.

Suy ra ba góc của tam giác ABC đều có số đo bằng 60°.

Vậy số đo các góc của tam giác ABC đều bằng 60°.